NOI2013 Day1
向量内积
题目描述:两个(d)维向量(A)与(B)的内积为其相对应维度的权值的乘积和,现有(n)个(d)维向量 ,求是否存在两个向量的内积为(k)((k=2,3))的倍数。
solution:
考虑(k=2),以下为在((mod 2))下运算,设矩阵(A_1,A_2),
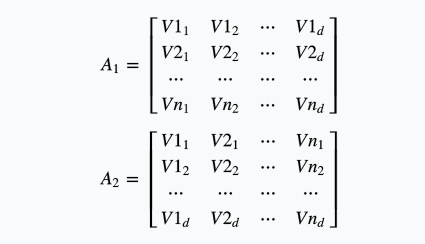
设矩阵(P=A_1 * A_2),若非对角线出现(0),则有一对内积为(0)
(P)对角线上的(0)要处理一下
设矩阵(F),令(F_{ii}+P_{ii}=1),其余为(0)
设矩阵(G)全为(1)
矩阵(T=G-F-P),问题转为求是否有一元素在(T)中为(1)
随机一(n * 1)矩阵(X),若(L=T * X,L_{i,1}=1),则(T_i)有一元素为(1)
(L=T * X=G * X-F * X-A_1 * (A_2 * X))
第一部分(O(n)), 第二部分(O(nd)),第三部分(O(nd))。
考虑(k=3),((mod 3)=0,1,2),因为(1 * 1=1(mod 3),2 * 2=1(mod 3)),所以将内积结果平方就可以了。
假设两个(d)维向量(A,B)
((A * B)^2=(A_1B_1+A_2B_2+ cdots +A_dB_d)(A_1B_1+A_2B_2+ cdots +A_dB_d))
(=(A_1A_1+A_1A_2+ cdots +A_1A_d+A_2A_1+ cdots +A_2A_d+ cdots +A_dA_d)*(B_1B_1+B_1B_2+ cdots +B_1B_d+B_2B_1+ cdots +B_2B_d+ cdots +B_dB_d))
所以只需要将(d)维扩展到(d^2)维即可, 以上操作均在((mod 3))下运算,所以只要(L)有非零就可以了。
时间复杂度:(O(nd^2))
树的计数
题目描述:给定一个 DFS 序和 BFS 序,求符合条件的有根树中,树的高度的平均值。
solution:
这题有点求期望值的味道。
根据(BFS)序对(DFS)序重标号。(pos[i])表示(i)在(DFS)的第几位,(deep[i])为(i)的深度
for (int i=1; i<=n; ++i) w[BFS[i]]=i;
for (int i=1; i<=n; ++i) DFS[i]=w[DFS[i]];
for (int i=1; i<=n; ++i) pos[DFS[i]]=i;
约束条件:
1、(1)为根
2、对于(BFS)连续的一段([L, R]),如果它们在同一层,必有(pos[L]<pos[L+1]<cdots<pos[R])
3、对于(DFS)的相邻两个数(d[i],d[i+1]),必有(deep[d[i+1]]leq deep[d[i]]+1)
设(s[i]),当(s[i]=1)时,(i)与(i+1)不在同一层,当(s[i]=0)时,可能在同一行也可能不在。
转化约束条件:
1、(s[i]=1)
2、若(pos[i+1]<pos[i],s[i]=1)
3、若(DFS[i]<DFS[i+1]),则(sum_{j=d[i]}^{d[i+1]-1} s[i]leq1)(若(DFS[i]>DFS[i+1]),从(BFS)得(deep[d[i+1]]leq deep[d[i]]))
用打标记的方法来表示某一段的(s[i])的值是否确定,不确定的(s[i])可以取(0,1)对答案的贡献为(0.5)。
因为(i+1)可以是(i)的儿子或兄弟要满足一下条件:
1、(i+1)为儿子时,(i)为所在层的最后一个,当(i+1)做兄弟时,(i+1)为所在层最后一个
2、其它不在(i)子树或(i+1)子树的点的深度均不超过(i),否则(BFS)有误。
以(i+1)为根的子树方案数是一定的,做儿子还是做兄弟只是多(1)的影响,所以贡献为(0.5)
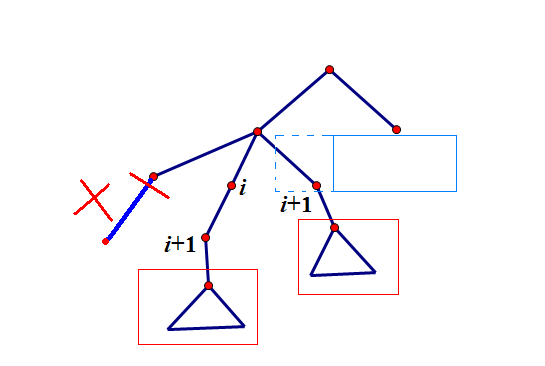
(蓝框内不能有点,红框方案相同,最左边错误)
#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include <deque>
#include <queue>
#include <vector>
#include <map>
#include <complex>
using namespace std;
const int maxn=int(2e5)+100;
typedef int arr[maxn];
int n;
arr DFS, BFS, w, x, mat, sum, pos;
double ans;
void init()
{
scanf("%d", &n);
for (int i=1; i<=n; ++i) scanf("%d", &DFS[i]);
for (int i=1; i<=n; ++i) scanf("%d", &BFS[i]);
for (int i=1; i<=n; ++i) w[BFS[i]]=i;
for (int i=1; i<=n; ++i) DFS[i]=w[DFS[i]];
for (int i=1; i<=n; ++i) pos[DFS[i]]=i;
}
void solve()
{
x[1]=1;
//mat用来标记那一段是确定的
mat[1]++; mat[2]--;
for (int i=1; i<n; ++i)
if (pos[i]>pos[i+1])
{
x[i]=1;
mat[i]++; mat[i+1]--;
}
for (int i=1; i<=n; ++i) sum[i]=sum[i-1]+x[i];
for (int i=1; i<n; ++i)
if (DFS[i]<DFS[i+1])
{
if (sum[DFS[i+1]-1]-sum[DFS[i]-1])
{
mat[DFS[i]]++;
mat[DFS[i+1]]--;
}
}
for (int i=1, cnt=0; i<n; ++i)
{
cnt+=mat[i];
if (cnt) ans+=x[i];//cnt>0说明s[i]是确定的
else ans+=0.5;
}
}
int main()
{
freopen("count.in", "r", stdin);
freopen("count.out", "w", stdout);
init();
solve();
printf("%.3lf
", ans+1.0);
return 0;
}
时间复杂度:(O(n))