题解-Infinite Path
(T) 组测试数据。每次给你一个 (n) 的排列 ({p_n}),以及排列中第 (i) 个数的颜色 (c_i)。
令两个排列 (A) 和 (B) 的乘积 (C=A imes B) 满足 (C_i=A_{B_i})。
对于排列 (p), (p^k=underbrace{p imes p imes cdots imes p}_{k p})。
求最小的 (k),使 (P=p^k) 中存在 (i) 满足 (c_i=c_{P_i}=c_{P_{P_i}}=cdots)。
数据范围:(1le Tle 10^4),(1le n,sum nle 2 imes 10^5)。
可以把每个 (p_i) 看做一条 (i o p_i) 的边。
因为 (p) 是个排列,所以会形成多个环,每个点每条边都在一个环上。
所以可以单独考虑每个环的最小 (k),然后答案取其最小值。
设当前环大小为 (sz):
(k) 每 (+1) 就使原来的边 (i o p^k_{i}) 变成了 (i o p^{k+1}_{i})。
设 (g=gcd(k,sz)),很明显 (p^k) 的图中每个环元素和 (p^g) 中的一样。
所以只需考虑 (k) 是 (sz) 的因数的情况:
每一整个大环会被分成 (frac{sz}{k}) 个环,环上相邻元素在原环上距离为 (k)。
然后对 (frac{sz}{k}) 个环判断是否颜色相等,如果有颜色相等的环,就说明对于该环该 (k) 是合法的。
然后枚举 (k),找到最小合法 (k) 即可。
时间复杂度 (Theta(nsigma(n)))((sigma(n)) 表示 (n) 的约数个数)。
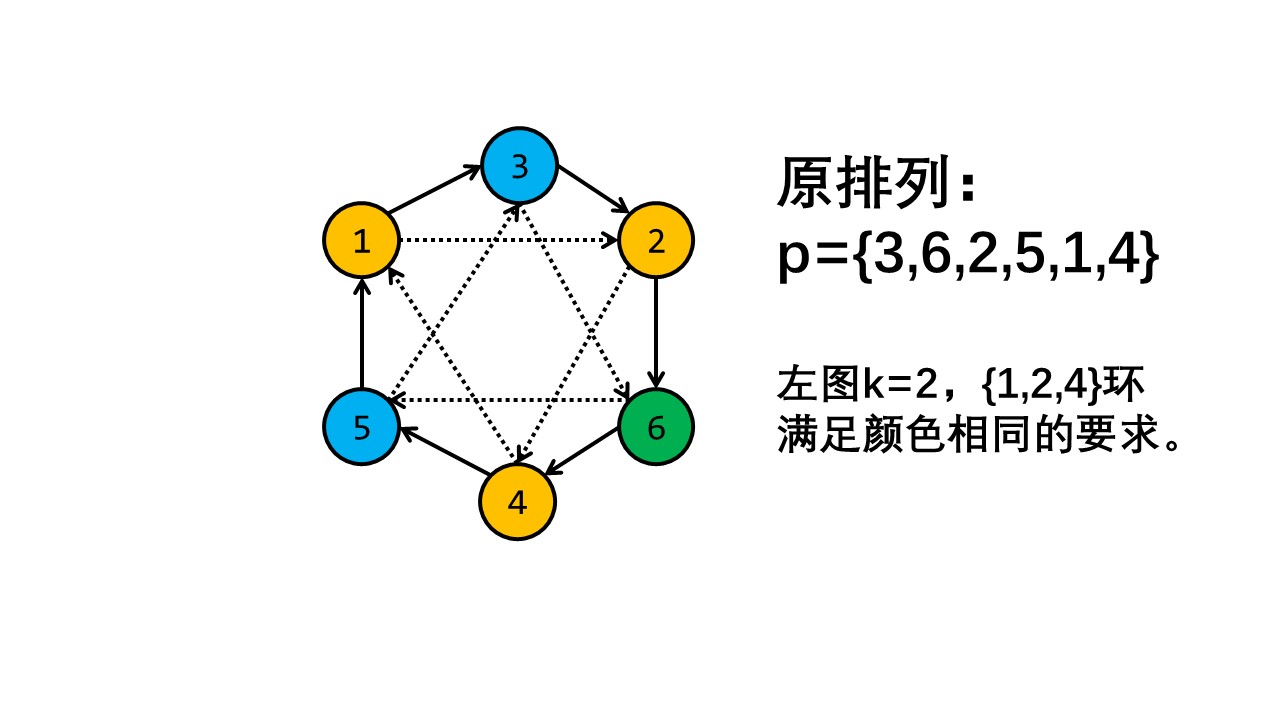
蒟蒻讲不清楚,放个只有一个环情况的例图:
( exttt{vector}) 代码实现:
#include <bits/stdc++.h>
using namespace std;
//&Start
#define re register
#define il inline
#define inf 0x3f3f3f3f
typedef long long lng;
//&Data
#define N 200000
bitset<N+5> vis;
//&Main
int main(){
re int t,n,ans;
scanf("%d",&t); //多组测试数据!
for(re int ti=1;ti<=t;ti++){
scanf("%d",&n);
vector<int> p(n+1),c(n+1);
for(re int i=1;i<=n;i++) scanf("%d",&p[i]);
for(re int i=1;i<=n;i++) scanf("%d",&c[i]);
vis.reset(),ans=inf;
for(re int i=1;i<=n;i++)if(!vis[i]){ //如果该点未出现于之前的环
vector<int> C,d; //C:该环上的点的颜色,d:sz的因素
for(re int j=i,f=1;f||j!=i;f=0,j=p[j]) C.push_back(c[j]),vis[j]=1;
re int sz=C.size(),K;
for(re int j=1;j<=sz;j++)if(sz%j==0) d.push_back(j);
for(re int k:d){
re int ok=0;
for(re int s=0;s<k;s++){
re int samc=1;
for(re int j=s;j<sz;j+=k)if(C[j]!=C[s]){samc=0;break;} //判断环上点颜色相等
if(samc){ok=1;break;}
}
if(ok){K=k;break;}
}
ans=min(ans,K); //取k最小值
}
printf("%d
",ans);
}
return 0;
}
祝大家学习愉快!