Little Mishka is a great traveller and she visited many countries. After thinking about where to travel this time, she chose XXX — beautiful, but little-known northern country.
Here are some interesting facts about XXX:
- XXX consists of n cities, k of whose (just imagine!) are capital cities.
- All of cities in the country are beautiful, but each is beautiful in its own way. Beauty value of i-th city equals to ci.
- All the cities are consecutively connected by the roads, including 1-st and n-th city, forming a cyclic route 1 — 2 — ... — n — 1. Formally, for every 1 ≤ i < n there is a road between i-th and i + 1-th city, and another one between 1-st and n-th city.
- Each capital city is connected with each other city directly by the roads. Formally, if city x is a capital city, then for every 1 ≤ i ≤ n, i ≠ x, there is a road between cities x and i.
- There is at most one road between any two cities.
- Price of passing a road directly depends on beauty values of cities it connects. Thus if there is a road between cities i and j, price of passing it equals ci·cj.
Mishka started to gather her things for a trip, but didn't still decide which route to follow and thus she asked you to help her determine summary price of passing each of the roads in XXX. Formally, for every pair of cities a and b (a < b), such that there is a road between a and b you are to find sum of products ca·cb. Will you help her?
The first line of the input contains two integers n and k (3 ≤ n ≤ 100 000, 1 ≤ k ≤ n) — the number of cities in XXX and the number of capital cities among them.
The second line of the input contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 10 000) — beauty values of the cities.
The third line of the input contains k distinct integers id1, id2, ..., idk (1 ≤ idi ≤ n) — indices of capital cities. Indices are given in ascending order.
Print the only integer — summary price of passing each of the roads in XXX.
4 1
2 3 1 2
3
17
5 2
3 5 2 2 4
1 4
71
This image describes first sample case:
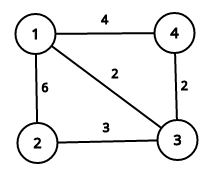
It is easy to see that summary price is equal to 17.
This image describes second sample case:
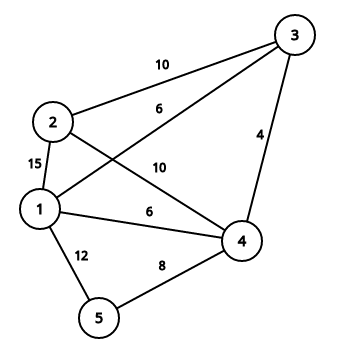
It is easy to see that summary price is equal to 71.
题目连接:http://codeforces.com/contest/703/problem/B
题意:n个城市,每个城市之间最多有一条道路直接相连。 1 — 2 — ... — n — 1之间有一条道路。其中k个城市是首都,首都与其他城市之间都有道路直接相连。输出这个城市所有道路的权值。
思路:n个城市的权值总和为sum,每个首都与其他城市之间的道路权值为c[i]*(sum-c[i-1]-c[i+1]-cou)。其中cou为c[i]之前出现过的首都的权值总和。考虑c[i-1]与c[i+1]在i=1和i=n的情况和cou里面包括了c[i-1]和c[i+1]的情况。
代码:

#include<bits/stdc++.h> using namespace std; __int64 c[100100]; int d[100100]; int sign[100100]; int main() { int i,n,k; scanf("%d%d",&n,&k); __int64 ans=0,sum=0; for(i=1; i<=n; i++) { scanf("%I64d",&c[i]); if(i>1) ans+=(c[i-1]*c[i]); sum+=c[i]; } ans+=(c[n]*c[1]); __int64 cou=0; memset(sign,0,sizeof(sign)); for(i=0; i<k; i++) { scanf("%d",&d[i]); __int64 flag=0; if(d[i]>1) { if(sign[d[i]-1]==0) flag+=c[d[i]-1]; } else { if(sign[n]==0) flag+=c[n]; } if(d[i]<n) { if(sign[d[i]+1]==0) flag+=c[d[i]+1]; } else { if(sign[1]==0) flag+=c[1]; } //cout<<c[d[i]]<<" "<<flag<<" "<<cou<<endl; ans+=c[d[i]]*(sum-flag-cou-c[d[i]]); cou+=c[d[i]]; sign[d[i]]=1; } printf("%I64d ",ans); return 0; }
