[算法模板]SOS DP
正文
SOS-DP(( ext{Sum over Subsets}))是用来解决这样的问题的:
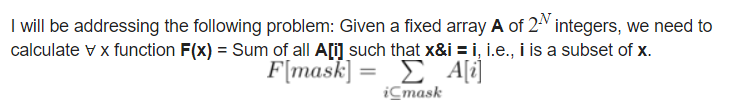
其实就是子集和DP。上面每个(F[mask])里面包含了(mask)所有二进制子集的信息。这是一种(nlog_2 n)的DP方法。
我们定义一个DP状态(S(mask,i))代表(mask)子集中只有最靠右的(i)位与其不同的状态。
具体是这样的:
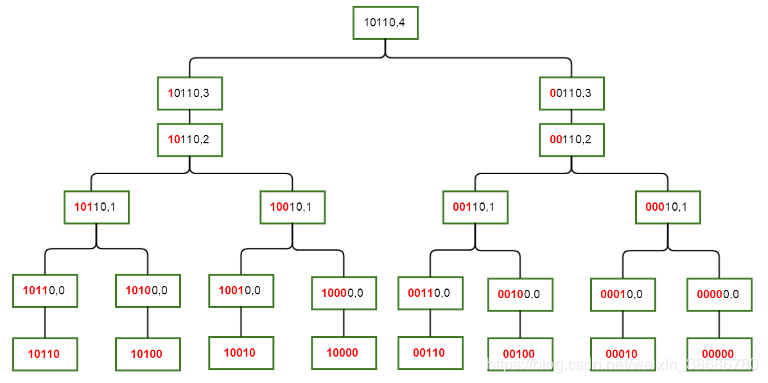
图中描述了(S(10110,4))这个状态和其所有儿子之间的关系。
形象一些解释就是每次我们求解一个状态时,我们只从他的所有子集里和他只差一位的状态转移过来。(众所周知,如果(Asubseteq B,Bsubseteq C)那么(Asubseteq) C)。
放一段代码:
for(int i = 0; i<(1<<N); ++i)
F[i] = A[i];
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
if(mask & (1<<i))
F[mask] += F[mask^(1<<i)];
}
所以显然,复杂度(Nspace 2^N)。如果令值域为(M),那么复杂度就是(Mlog_2M)。
例题
参考资料
SOS Dynamic Programming [Tutorial]
