1. 概述
卷积神经网络是一种特殊的深层的神经网络模型,它的特殊性体现在两个方面,一方面它的神经元间的连接是非全连接的, 另一方面同一层中某些神经元之间的连接的权重是共享的(即相同的)。它的非全连接和权值共享的网络结构使之更类似于生物 神经网络,降低了网络模型的复杂度(对于很难学习的深层结构来说,这是非常重要的),减少了权值的数量。
卷积网络最初是受视觉神经机制的启发而设计的,是为识别二维形状而设计的一个多层感知器,这种网络结构对平移、比例缩放、倾斜或者共他 形式的变形具有高度不变性。1962年Hubel和Wiesel通过对猫视觉皮层细胞的研究,提出了感受野(receptive field)的概念,1984年日本学者Fukushima 基于感受野概念提出的神经认知机(neocognitron)模型,它可以看作是卷积神经网络的第一个实现网络,也是感受野概念在人工神经网络领域的首次应用。
神经认知机将一个视觉模式分解成许多子模式(特征),然后进入分层递阶式相连的特征平面进行处理,它试图将视觉系统模型化,使其能够在即使物体有 位移或轻微变形的时候,也能完成识别。神经认知机能够利用位移恒定能力从激励模式中学习,并且可识别这些模式的变化形。在其后的应用研究中,Fukushima 将神经认知机主要用于手写数字的识别。随后,国内外的研究人员提出多种卷积神经网络形式,在邮政编码识别(Y. LeCun etc)、车牌识别和人脸识别等方面 得到了广泛的应用。
2. CNN的结构
卷积网络是为识别二维形状而特殊设计的一个多层感知器,这种网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。 这些良好的性能是网络在有监督方式下学会的,网络的结构主要有稀疏连接和权值共享两个特点,包括如下形式的约束:
1 特征提取。每一个神经元从上一层的局部接受域得到突触输人,因而迫使它提取局部特征。一旦一个特征被提取出来, 只要它相对于其他特征的位置被近似地保留下来,它的精确位置就变得没有那么重要了。
2 特征映射。网络的每一个计算层都是由多个特征映射组成的,每个特征映射都是平面形式的。平面中单独的神经元在约束下共享 相同的突触权值集,这种结构形式具有如下的有益效果:a.平移不变性。b.自由参数数量的缩减(通过权值共享实现)。
3.子抽样。每个卷积层跟着一个实现局部平均和子抽样的计算层,由此特征映射的分辨率降低。这种操作具有使特征映射的输出对平移和其他 形式的变形的敏感度下降的作用。
2.1 稀疏连接(Sparse Connectivity)
卷积网络通过在相邻两层之间强制使用局部连接模式来利用图像的空间局部特性,在第m层的隐层单元只与第m-1层的输入单元的局部区域有连接,第m-1层的这些局部 区域被称为空间连续的接受域。我们可以将这种结构描述如下:
设第m-1层为视网膜输入层,第m层的接受域的宽度为3,也就是说该层的每个单元与且仅与输入层的3个相邻的神经元相连,第m层与第m+1层具有类似的链接规则,如下图所示。
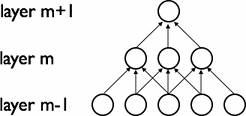
可以看到m+1层的神经元相对于第m层的接受域的宽度也为3,但相对于输入层的接受域为5,这种结构将学习到的过滤器(对应于输入信号中被最大激活的单元)限制在局部空间 模式(因为每个单元对它接受域外的variation不做反应)。从上图也可以看出,多个这样的层堆叠起来后,会使得过滤器(不再是线性的)逐渐成为全局的(也就是覆盖到了更 大的视觉区域)。例如上图中第m+1层的神经元可以对宽度为5的输入进行一个非线性的特征编码。
2.2 权值共享(Shared Weights)
在卷积网络中,每个稀疏过滤器hihi通过共享权值都会覆盖整个可视域,这些共享权值的单元构成一个特征映射,如下图所示。
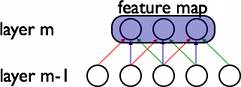
在图中,有3个隐层单元,他们属于同一个特征映射。同种颜色的链接的权值是相同的,我们仍然可以使用梯度下降的方法来学习这些权值,只需要对原始算法做一些小的改动, 这里共享权值的梯度是所有共享参数的梯度的总和。我们不禁会问为什么要权重共享呢?一方面,重复单元能够对特征进行识别,而不考虑它在可视域中的位置。另一方面,权值 共享使得我们能更有效的进行特征抽取,因为它极大的减少了需要学习的自由变量的个数。通过控制模型的规模,卷积网络对视觉问题可以具有很好的泛化能力。
2.3 The Full Model
卷积神经网络是一个多层的神经网络,每层由多个二维平面组成,而每个平面由多个独立神经元组成。网络中包含一些简单元和复杂元,分别记为S-元 和C-元。S-元聚合在一起组成S-面,S-面聚合在一起组成S-层,用Us表示。C-元、C-面和C-层(Us)之间存在类似的关系。网络的任一中间级由S-层与C-层 串接而成,而输入级只含一层,它直接接受二维视觉模式,样本特征提取步骤已嵌入到卷积神经网络模型的互联结构中。
一般地,Us为特征提取层,每个神经元的输入与前一层的局部感受野相连,并提取该局部的特征,一旦该局部特征被提取后,它与其他特征间的位置关系 也随之确定下来;Uc是特征映射层,网络的每个计算层由多个特征映射组成,每个特征映射为一个平面,平面上所有神经元的权值相等。特征映射结构采用 影响函数核小的sigmoid函数作为卷积网络的激活函数,使得特征映射具有位移不变性(这一句表示没看懂,那位如果看懂了,请给我讲解一下)。此外,由于 一个映射面上的神经元共享权值,因而减少了网络自由参数的个数,降低了网络参数选择的复杂度。卷积神经网络中的每一个特征提取层(S-层)都紧跟着一个 用来求局部平均与二次提取的计算层(C-层),这种特有的两次特征提取结构使网络在识别时对输入样本有较高的畸变容忍能力。
下图是一个卷积网络的实例
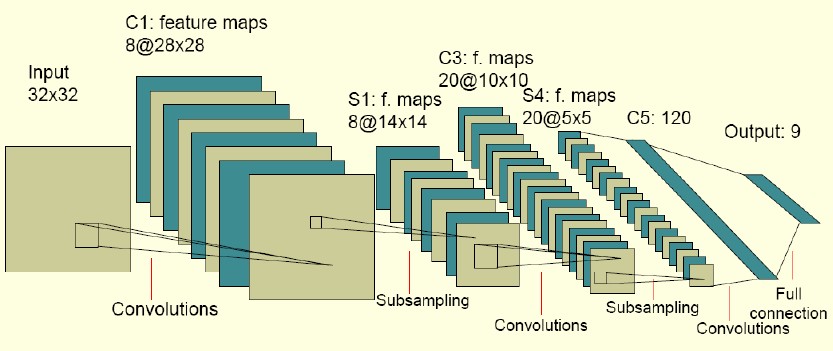
图中的卷积网络工作流程如下,输入层由32×32个感知节点组成,接收原始图像。然后,计算流程在卷积和子抽样之间交替进行,如下所 述:第一隐藏层进行卷积,它由8个特征映射组成,每个特征映射由28×28个神经元组成,每个神经元指定一个 5×5 的接受域;第二隐藏层实现子 抽样和局部平均,它同样由 8 个特征映射组成,但其每个特征映射由14×14 个神经元组成。每个神经元具有一个 2×2 的接受域,一个可训练 系数,一个可训练偏置和一个 sigmoid 激活函数。可训练系数和偏置控制神经元的操作点。第三隐藏层进行第二次卷积,它由 20 个特征映射组 成每个特征映射由 10×10 个神经元组成。该隐藏层中的每个神经元可能具有和下一个隐藏层几个特征映射相连的突触连接,它以与第一个卷积 层相似的方式操作。第四个隐藏层进行第二次子抽样和局部平均汁算。它由 20 个特征映射组成,但每个特征映射由 5×5 个神经元组成,它以 与第一次抽样相似的方式操作。第五个隐藏层实现卷积的最后阶段,它由 120 个神经元组成,每个神经元指定一个 5×5 的接受域。最后是个全 连接层,得到输出向量。相继的计算层在卷积和抽样之间的连续交替,我们得到一个“双尖塔”的效果,也就是在每个卷积或抽样层,随着空 间分辨率下降,与相应的前一层相比特征映射的数量增加。卷积之后进行子抽样的思想是受到动物视觉系统中的“简单的”细胞后面跟着“复 杂的”细胞的想法的启发而产生的。
图中所示的多层感知器包含近似 100000 个突触连接,但只有大约2600 个自由参数。自由参数在数量上显著地减少是通过权值共享获得 的,学习机器的能力(以 VC 维的形式度量)因而下降,这又提高它的泛化能力。而且它对自由参数的调整通过反向传播学习的随机形式来实 现。另一个显著的特点是使用权值共享使得以并行形式实现卷积网络变得可能。这是卷积网络对全连接的多层感知器而言的另一个优点。
3. CNN的学习
总体而言,前面提到的卷积网络可以简化为下图所示模型:
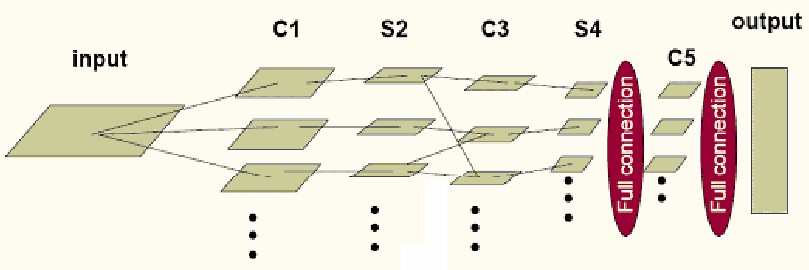
其中,input 到C1、S4到C5、C5到output是全连接,C1到S2、C3到S4是一一对应的连接,S2到C3为了消除网络对称性,去掉了一部分连接, 可以让特征映射更具多样性。需要注意的是 C5 卷积核的尺寸要和 S4 的输出相同,只有这样才能保证输出是一维向量。
3.1 卷积层的学习
卷积层的典型结构如下图所示。
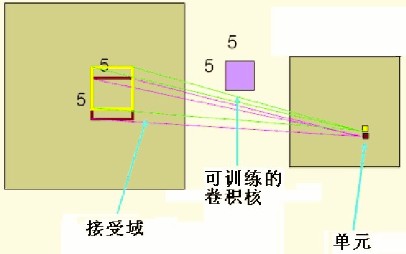
卷积层的前馈运算是通过如下算法实现的:
卷积层的输出= Sigmoid( Sum(卷积) +偏移量)其中卷积核和偏移量都是可训练的。下面是其核心代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
ConvolutionLayer::fprop(input,output) {
//取得卷积核的个数
int n=kernel.GetDim(0);
for (int i=0;i<n;i++) {
//第i个卷积核对应输入层第a个特征映射,输出层的第b个特征映射
//这个卷积核可以形象的看作是从输入层第a个特征映射到输出层的第b个特征映射的一个链接
int a=table[i][0], b=table[i][1];
//用第i个卷积核和输入层第a个特征映射做卷积
convolution = Conv(input[a],kernel[i]);
//把卷积结果求和
sum[b] +=convolution;
}
for (i=0;i<(int)bias.size();i++) {
//加上偏移量
sum[i] += bias[i];
}
//调用Sigmoid函数
output = Sigmoid(sum);
}
|
其中,input是 n1×n2×n3 的矩阵,n1是输入层特征映射的个数,n2是输入层特征映射的宽度,n3是输入层特征映射的高度。output, sum, convolution, bias是n1×(n2-kw+1)×(n3-kh+1)的矩阵,kw,kh是卷积核的宽度高度(图中是5×5)。kernel是卷积核矩阵。table是连接表,即如果第a输入和第b个输出之间 有连接,table里就会有[a,b]这一项,而且每个连接都对应一个卷积核。
卷积层的反馈运算的核心代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
ConvolutionLayer::bprop(input,output,in_dx,out_dx) {
//梯度通过DSigmoid反传
sum_dx = DSigmoid(out_dx);
//计算bias的梯度
for (i=0;i<bias.size();i++) {
bias_dx[i] = sum_dx[i];
}
//取得卷积核的个数
int n=kernel.GetDim(0);
for (int i=0;i<n;i++)
{
int a=table[i][0],b=table[i][1];
//用第i个卷积核和第b个输出层反向卷积(即输出层的一点乘卷积模板返回给输入层),并把结果累加到第a个输入层
input_dx[a] += DConv(sum_dx[b],kernel[i]);
//用同样的方法计算卷积模板的梯度
kernel_dx[i] += DConv(sum_dx[b],input[a]);
}
}
|
其中in_dx,out_dx 的结构和 input,output 相同,代表的是相应点的梯度。
3.2 子采样层的学习
子采样层的典型结构如下图所示。

类似的字采样层的输出的计算式为:
输出= Sigmoid( 采样*权重 +偏移量)其核心代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
SubSamplingLayer::fprop(input,output) {
int n1= input.GetDim(0);
int n2= input.GetDim(1);
int n3= input.GetDim(2);
for (int i=0;i<n1;i++) {
for (int j=0;j<n2;j++) {
for (int k=0;k<n3;k++) {
//coeff 是可训练的权重,sw 、sh 是采样窗口的尺寸。
sub[i][j/sw][k/sh] += input[i][j][k]*coeff[i];
}
}
}
for (i=0;i<n1;i++) {
//加上偏移量
sum[i] = sub[i] + bias[i];
}
output = Sigmoid(sum);
}
|
子采样层的反馈运算的核心代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
SubSamplingLayer::bprop(input,output,in_dx,out_dx) {
//梯度通过DSigmoid反传
sum_dx = DSigmoid(out_dx);
//计算bias和coeff的梯度
for (i=0;i<n1;i++) {
coeff_dx[i] = 0;
bias_dx[i] = 0;
for (j=0;j<n2/sw;j++)
for (k=0;k<n3/sh;k++) {
coeff_dx[i] += sub[j][k]*sum_dx[i][j][k];
bias_dx[i] += sum_dx[i][j][k]);
}
}
for (i=0;i<n1;i++) {
for (j=0;j<n2;j++)
for (k=0;k<n3;k++) {
in_dx[i][j][k] = coeff[i]*sum_dx[i][j/sw][k/sh];
}
}
}
|
3.3 全连接层的学习
全连接层的学习与传统的神经网络的学习方法类似,也是使用BP算法,这里就不详述了。
关于CNN的完整代码可以参考https://github.com/ibillxia/DeepLearnToolbox/tree/master/CNN中的Matlab代码。
References
[1] Learn Deep Architectures for AI, Chapter 4.5.
[2] Deep Learning Tutorial, Release 0.1, Chapter 6.
[3] Convolutional Networks for Images Speech and Time-Series.
[4] 基于卷积网络的三维模型特征提取. 王添翼.
[5] 卷积神经网络的研究及其在车牌识别系统中的应用. 陆璐.





