声明
-
之前虽然听过压缩感知和稀疏表示,实际上前两天才正式着手开始了解,纯属新手,如有错误,敬请指出,共同进步。
-
主要学习资料是 Coursera 上 Duke 大学的公开课——Image and video processing, by Pro.Guillermo Sapiro 第 9 课。
-
由于对图像处理的了解也来自与该课程,没正经儿看过几本图像方面的书籍,有些术语只能用视频中的英文来表达,见谅哈!
1. From Local to Global Treatment
图片尺寸有大有小,在 DCT 变换中,我们一般取 8×8 的方块作为一组 64 维的变换信号,在稀疏表示中,我们同样也不能把整张图片作为 X^T 矩阵,而是在大图片中取一定尺寸的 patch (假设是 8×8 的方块)作为一个 signal。对于图片中的所有的 patch (假设 ij 是 patch 的左上角坐标)组成的信号,已知字典 D 和噪声图片 y ,估计公式如下:

y: 带有噪音的图片—— the whole image
x: 要恢复的 clear image
Rij x: 以 i,j 为左上角坐标的 patch, Rij 是从 x 中提取 patch 的 0-1 矩阵
D: 字典 for all the overlapping patches
字典 D 从哪里学习?第一种选择是基于图片的数据库,第二种是直接使用要降噪的图片进行训练。还有一种可能性是:首先基于图片的数据库得到字典 D (off-line),接着来了一张要降噪的图片,我们的做法是新建一个以 D 为初始化的字典,在要处理的图片上再进行迭代(on-line),得到新字典,这个新字典更适合降噪,代价是多一些计算。
2. K-SVD Image Denoising
在上一小节中,我们提出的可能性是 D 也需要根据要降噪的图片进行再适应,所以,图片降噪的公式多了一参数:

有三个变量,处理方法是先固定其中两个,优化一个,然后迭代。从整体上来说,先用 K-SVD 算法得到字典矩阵 D 和系数编码 alpha,保持它们不动,再优化 x:

x 的最优解实际上就是所有包含 x 像素点的 patch 的平均值,比如 patch 的大小是 8×8, 那么包含图片中某一个像素点的 patch 就有 64 个,这个像素点最优解就是取这 64 个patch 对应位置的平均值。当然,你也可以用权重来调节不同位置的 patch 对 pixel 的影响,比如 pixel 在中间的 patch,权重大,pixel 在 patch 边边角角的地方,权重小。
3. Compressed Sensing
前面我们探讨了 sparse represent 的等式,这里主要讲 compressed sensing 的概念,即在稀疏表示的等号两边同时乘以矩阵 Q:
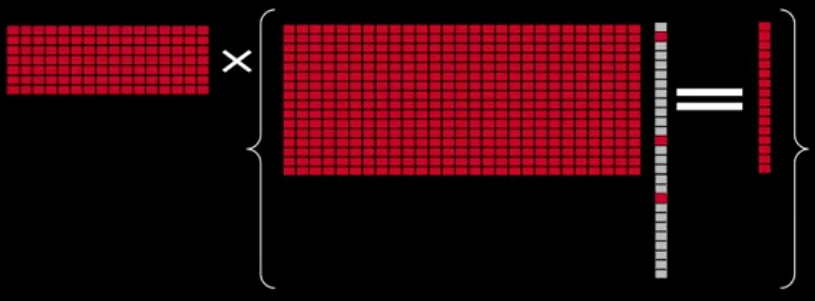
就变成了:
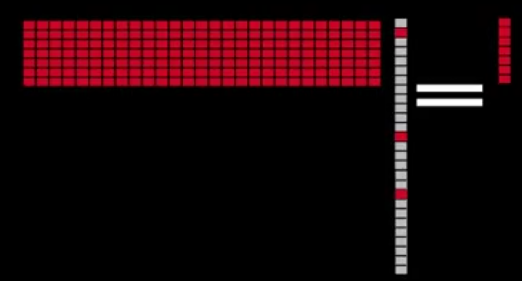
用公式可以表达为:
![]()
可以看到,变换后的信号被大大压缩了。在一直 x波浪 和 D波浪 的情况下求 alpha 这个问题和前面 sparse coding 非常类似。一个关键问题是:在什么条件下由已知信号 x波浪 的情况下恢复稀疏表示 alpha?显然,这个问题与矩阵 Q,字典 D 和 alpha 的 sparse level 有关,背后涉及很多数学理论。
4. Structured Sparse Models and GMM
待续...
5. Sparse Modeling and Classification-Activity Recognition
待续...