Python实现栈

栈（stack）又名堆栈，它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。

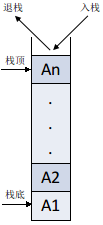
栈允许进行插入和删除操作的一端称为栈顶(top)，另一端为栈底(bottom)；栈底固定，而栈顶浮动；栈中元素个数为零时称为空栈。插入一般称为进栈（PUSH），删除则称为退栈（POP）。

由于堆叠数据结构只允许在一端进行操作，因而按照后进先出（LIFO, Last In First Out）的原理运作。栈也称为后进先出表。

栈的演示

Visualgo这个网站，我们可以看到整个数据结构的变化过程。可以通过左下角的按钮调慢演示过程。可能也自己动手 code 实现了过程，那么再在网站上演示一下元素的各种操作过程，会带来一些更直观的印象。

复杂度分析

栈属于常见的一种线性结构，对于进栈和退栈而言，时间复杂度都为 O(1)

在接下来的内容里，我们将逐步介绍栈的具体功能是如何实现的。

1. 创建一个 Stack 的类

对栈进行初始化参数设计

具体实现代码如下：

class Stack(object):
    def __init__(self, limit=10):
        self.stack = [] #存放元素
        self.limit = limit #栈容量极限

2. push 进栈

压入 push ：将新元素放在栈顶

当新元素入栈时，栈顶上移，新元素放在栈顶。

具体实现代码如下:

   def push(self, data):
        if len(self.stack) >= self.limit: #判断栈是否溢出
            print('StackOverflowError')
            pass
        self.stack.append(data)

3. pop 退栈

弹出 pop ：从栈顶移出一个数据

• 栈顶元素拷贝出来
• 栈顶下移
• 拷贝出来的栈顶作为函数返回值

具体实现代码如下:

    def pop(self):
        if self.stack:
            return self.stack.pop()
        else:
            raise IndexError('pop from an empty stack') #空栈不能被弹出

4. 添加其他函数

peek : 查看堆栈的最上面的元素

is_empty : 判断栈是否为空

size : 返回栈的大小

具体实现代码如下：

    def peek(self):
        if self.stack:
            return self.stack[-1]
    def is_empty(self):
        return not bool(self.stack)
    def size(self):
        return len(self.stack)

完整代码如下：

class Stack(object):
    def __init__(self, limit=10):
        self.stack = [] #存放元素
        self.limit = limit #栈容量极限
    def push(self, data): #判断栈是否溢出
        if len(self.stack) >= self.limit:
            print('StackOverflowError')
            pass
        self.stack.append(data)
    def pop(self):
        if self.stack:
            return self.stack.pop()
        else:
            raise IndexError('pop from an empty stack') #空栈不能被弹出
    def peek(self): #查看堆栈的最上面的元素
        if self.stack:
            return self.stack[-1]
    def is_empty(self): #判断栈是否为空
        return not bool(self.stack)
    def size(self): #返回栈的大小
        return len(self.stack)

Stack（栈）在教科书中有一些非常经典的应用，例如：

• 一些其他有趣的应用程序但没有用于教学目的
• 括号匹配
• 后缀计算器

作业：检查括号是否完全匹配

使用一个堆栈检查括号字符串是否平衡

有效括号字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。
• 注意空字符串可被认为是有效字符串。

举例：

((())): True

((()): False

(())): False

目标：

1. 使用一个堆栈作为数据结构
2. 来检查括号字符串是否完全匹配

class Stack(object):
    def __init__(self, limit=10):
        self.stack = [] #存放元素
        self.limit = limit #栈容量极限
    def push(self, data): #判断栈是否溢出
        if len(self.stack) >= self.limit:
            print('StackOverflowError')
            pass
        self.stack.append(data)
    def pop(self):
        if self.stack:
            return self.stack.pop()
        else:
            raise IndexError('pop from an empty stack') #空栈不能被弹出
    def peek(self): #查看堆栈的最上面的元素
        if self.stack:
            return self.stack[-1]
    def is_empty(self): #判断栈是否为空
        return not bool(self.stack)
    def size(self): #返回栈的大小
        return len(self.stack)
def balanced_parentheses(parentheses):
    stack = Stack(len(parentheses))
    for parenthesis in parentheses:
        if parenthesis == '(':
            stack.push(parenthesis)
        elif parenthesis == ')':
            if stack.is_empty():
                return False
            stack.pop()
    return stack.is_empty()
if __name__ == '__main__':
    examples = ['((()))', '((())', '(()))']
    print('Balanced parentheses demonstration:
')
    for example in examples:
        print(example + ': ' + str(balanced_parentheses(example)))