P1020 [NOIP1999 普及组] 导弹拦截

第一问,单个系统最多能拦截多少导弹,求最长不升序列即可.

拿出LIS的模板涂涂改改.

bool cmp(const int& a, const int& b) { return a > b; }    

for (int i = 1; i <= n; i++)
        if (s[i] <= dp[len] || !len)
            dp[++len] = s[i];
        else {
            int x = upper_bound(dp + 1, dp + len, s[i], cmp) - dp;
            dp[x] = max(s[i], dp[i]);
        }
    printf("%d
", len);

第二问,最少需要多少个独立的系统拦截所有导弹.

导弹的高度是有相同的,先简化为所有数据不同.

首先猜想让一套系统取走序列的LDS(最长下降子序列),然后再来一套系统取走现在的序列的LDS,直至序列为空,得到使用的系统数量.这个方法我没有想到证明或者证伪的思路.

现在换一种思路,利用导弹是依次 飞来的条件,第一颗导弹X飞来时有一套装置A拦截之,现在第二颗导弹飞来,有:

1. 第二颗导弹比第一颗高:只能使用另一套装置B拦截.
2. 比第一颗低:可以使用装置A拦截,也可以使用装置B拦截.

如果明确第二种情况下选择的方法,那么至少可以模拟出来.先比较一下两种选项的利弊:

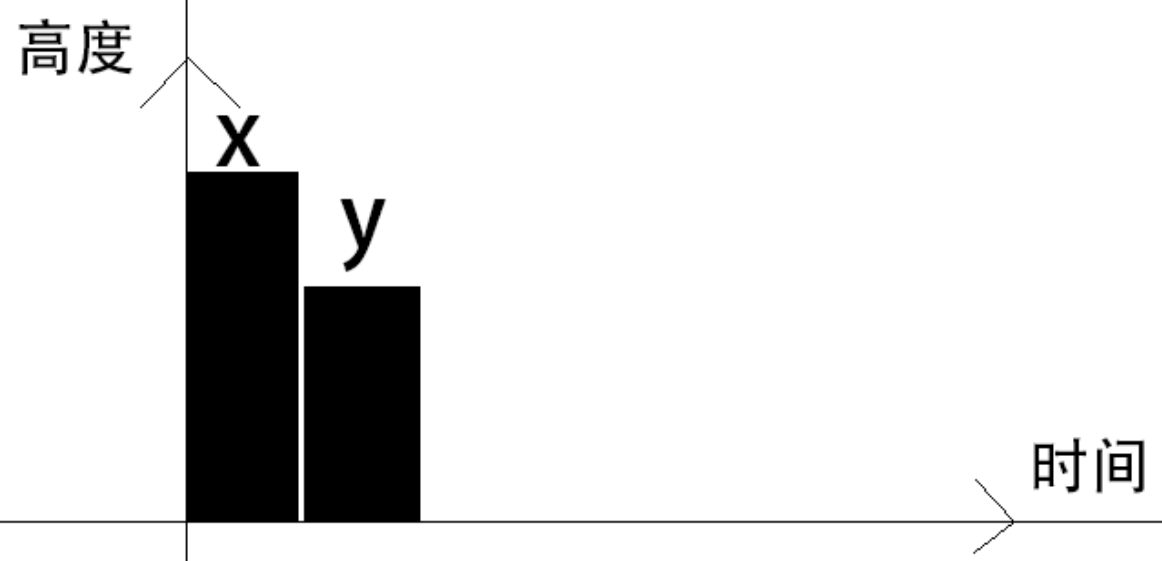
1. 使用A拦截第二颗导弹Y:"消耗"了一套系统,并使得A系统抛弃了高度位于X与Y之间的后续导弹,但仍可拦截高度低于Y的后续导弹.
2. 使用B拦截:"消耗了"两套系统,并使得A系统仍可拦截高度位于X与Y之间的后续导弹,且B系统可拦截高度低于Y的后续导弹.

现在"控制变量"一下,让情况1加一套系统,那么就变成了"消耗"了两套系统,并使得A系统抛弃了高度位于X与Y之间的后续导弹,但仍可拦截高度低于Y的后续导弹.且新增B系统可以补充拦截X与Y之间的后续导弹.可见情况1下可以在相同消耗的情况下达到等价情况2的效果.

然而在一种特殊情况下,情况1可以在更小消耗下达到等价情况2的效果:后续导弹高度均低于Y.此时情况1只需要消耗一套系统,情况2则消耗了至少两套系统.并且不存在这样一种特殊情况,使得情况2可以在消耗更小的条件下达到等价情况1的效果.

因此有如下求解策略:不停地启用一套新的系统,对于每一套系统依次尝试拦截所有导弹,如果可拦截则拦截,否则放弃,直到拦截所有的导弹.

按照这个策略即可求解出最小消耗系统数,且这个数值与该导弹高度序列的最长上升子序列的长度相等,证明可以看这里.这样才能保证复杂度.