首先排除暴力枚举.
如果把平面分割为两个平面,分别求出其中的最近点对的距离,再考虑两点分别在两个平面内部的情况,相比暴力枚举就省去了很多不必要的检查.

假设在左右平面里分别求最近点对的距离并取两者最小值得d,那么现在要检查是否存在分别位于左右平面的两点有更短的距离,那么只需要检查下图红线内的点:
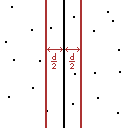
某一平面中在两条红线以外并且与另一平面中某点构成距离小于d的点是显然不存在的.
要检查红线内部且跨越两平面的最近点对问题,这题可以简单的转化为规模更大但处理更简单的问题:寻找红线内的最近点对距离,不要求跨越两平面.这里使用了如下算法:
①将区域内的点按照y坐标升序排列.初始化这个区域内的ans_mid为d.(或者INF,等效)
②依次对y最小到最大的每一个点,顺序枚举其上方的点(从而枚举的点的y坐标是非递减的),求出距离并更新ans_mid,如果这个过程中发现距离超过ans_mid了,break.
这个方法保证不会发现在同一侧的两点有着小于d的距离.某个点枚举到同侧点不会对答案造成影响,所以小于d的ans_mid只可能出现在位于不同侧的两点之间.
以上过程把原始问题分解为了三个问题:左侧内部的解,右侧内部的解,跨越左右侧的中间区域的解.并且这时已经求出了中间区域的解.
现在的问题是求解两个面积是原始问题面积一半的平面内的解.不断地这样分治下去,最终会达到一种情况,使得平面内只有两个点/一个点,这时直接返回两点间的距离/INF即可.后者是由于此规模下的问题无意义,返回INF以避免造成影响.
代码实现起来没有想象的那么困难.
#include <algorithm> #include <cmath> #include <cstdio> #include <cstring> #include <iostream> using namespace std; #define INF 1e9 + 1 typedef pair<double, double> PDD; int n; PDD s[200010], tmp[200010]; double dist(PDD a, PDD b) { double dx = a.first - b.first, dy = a.second - b.second; return sqrt(dx * dx + dy * dy); } bool cmpY(PDD a, PDD b) { return a.second < b.second; } double solve(int l, int r) { if (l == r) return INF; if (l + 1 == r) return dist(s[l], s[r]); double ans = INF; int mid = l + r >> 1; ans = min(solve(l, mid), solve(mid + 1, r)); int idx = 0; // 这里选择出位于中间区域的点, 实践表明用lower/upper_bound不如直接枚举来得快 for (int i = l; i <= r; i++) if (s[i].first >= s[mid].first - ans && s[i].first <= s[mid].first + ans) tmp[++idx] = s[i]; sort(tmp + 1, tmp + 1 + idx, cmpY); for (int i = 1; i <= idx - 1; i++) for (int j = 1; j + i <= idx; j++) { double d = dist(tmp[i], tmp[i + j]); if (d >= ans) break; else ans = d; } return ans; } int main() { // freopen("in2.txt", "r", stdin); scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%lf%lf", &s[i].first, &s[i].second); sort(s + 1, s + 1 + n); printf("%.4f ", solve(1, n)); return 0; }