poj 1753 Flip Game

题目连接

http://poj.org/problem?id=1753

Flip Game

Description

Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces, thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules: 

1. Choose any one of the 16 pieces. 
2. Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).

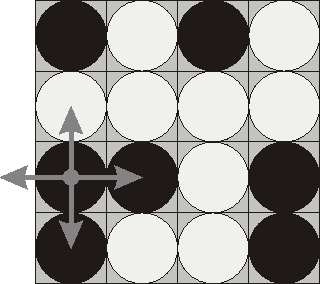Consider the following position as an example: 

bwbw 
wwww 
bbwb 
bwwb 
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become: 

bwbw 
bwww 
wwwb 
wwwb 
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal. 

Input

The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.

Output

Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible" (without quotes).

Sample Input

bwbw
wwww
bbwb
bwwb
bwwb
bbwb
bwwb
bwww
wwww
wwww
wwww
wwww
bbbb
bbbb
bbbb
bbbb
bbbb
bwbb
bbbb
bbbb
bwbb
bwbb
bwbb
bbbb
bwbb
wwwb
bwbb
bbbb
wwww
wwwb
wwbb
wwwb
wwww
wwww
wwwb
wwbb
wbwb
bwbw
wbwb
bwbw
bbbb
bwwb
bwwb
bbbb
bwwb
wbbw
wbbw
bwwb
bbww
bbww
wwbb
wwbb
bbwb
bbbw
wwbb
wwwb
wwwb
wwbw
wbww
wwbw
bbbb
wwww
wwbb
wbbb
bwwb
wbwb
wbbb
wbbb
bwbb
bwbb
bwbw
bbbw
wbwb
bbbb
bbww
wbbb
bbwb
bbbb
wbwb
bbbb

Sample Output

Impossible
4
0
0
Impossible
Impossible
1
1
1
Impossible
4
4
Impossible
Impossible
Impossible
Impossible
4
5
6
5

数据很小直接爆搜。。

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<vector>
#include<map>
using std::min;
using std::find;
using std::pair;
using std::swap;
using std::vector;
using std::multimap;
#define pb(e) push_back(e)
#define sz(c) (int)(c).size()
#define mp(a, b) make_pair(a, b)
#define all(c) (c).begin(), (c).end()
#define iter(c) __typeof((c).begin())
#define cls(arr, val) memset(arr, val, sizeof(arr))
#define cpresent(c, e) (find(all(c), (e)) != (c).end())
#define rep(i, n) for(int i = 0; i < (int)n; i++)
#define tr(c, i) for(iter(c) i = (c).begin(); i != (c).end(); ++i)
const int N = 1000000;
const int INF = 0x3f3f3f3f;
bool vis[N >> 2];
struct Node {
    int s;
    bool mat[4][4];
}que[N];
const int dx[] = { 0, 0, 0, -1, 1, }, dy[] = { 0, -1, 1, 0, 0, };
inline int hash(Node &x) {
    int ret = 0, k = 1;
    rep(i, 4) {
        rep(j, 4) {
            ret += k * x.mat[i][j];
            k <<= 1;
        }
    }
    return (ret + N) % N;
}
void bfs() {
    int lb = 0, ub = 1, v = hash(que[0]);
    if(!v || v == 65535) { puts("0"); return; }
    que[0].s = 1, cls(vis, false), vis[v] = true;
    while(lb != ub) {
        Node &x = que[lb++];
        rep(i, 4) {
            rep(j, 4) {
                Node t = x;
                rep(k, 5) {
                    int nx = dx[k] + i, ny = dy[k] + j;
                    if(nx < 0 || nx > 3 || ny < 0 || ny > 3) continue;
                    t.mat[nx][ny] ^= 1;
                }
                t.s = x.s + 1;
                v = hash(t);
                if(!v || v == 65535) { printf("%d
", x.s); return; }
                if(vis[v]) continue;
                vis[v] = true;
                que[ub++] = t;
            }
        }
    }
    puts("Impossible");
}
int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w+", stdout);
#endif
    char buf[10];
    while(~scanf("%s", buf)) {
        rep(i, 4) {
            if(i) scanf("%s", buf);
            rep(j, 4) {
                que[0].mat[i][j] = buf[j] == 'b' ? 1 : 0;
            }
        }
        bfs();
    }
    return 0;
}