题目描述
给出一棵树,定义一个点到一条路径的距离为这个点到这条路径上所有点的距离的最小值。求一条长度不超过s的路径,使得所有点到这条路径的距离的最大值最小。
输入
包含n行: 第1行,两个正整数n和s,中间用一个空格隔开。其中n为树网结点的个数,s为树网的核的长度的上界。设结点编号依次为1, 2, ..., n。 从第2行到第n行,每行给出3个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。例如,“2 4 7”表示连接结点2与4的边的长度为7。 所给的数据都是正确的,不必检验。
输出
只有一个非负整数,为指定意义下的最小偏心距。
样例输入
5 2
1 2 5
2 3 2
2 4 4
2 5 3
样例输出
5
题解
树的直径+双指针法+单调队列
首先易证路径一定在树的直径上(容易使用反证法证明)。
那么可以找出树的直径,然后考虑答案是怎么得到的:
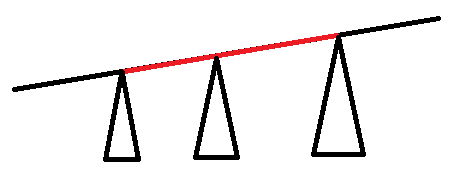
(上边的直线是直径,红色的为选定路径)
由于保证了是直径,因此路径左边的贡献只有直径左端点到路径左端点,路径右边的贡献只有直径右端点到路径右端点;路径中的贡献为子树(图中三角形)中最远的点。
那么可以处理出每个点除直径的子树内最远的点作为每个点的权值。
然后考虑:随着左端点的移动,右端点的决策位置是单调不降的。因此可以使用双指针法并用单调队列维护区间最大值。
时间复杂度$O(n)$
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 500010
using namespace std;
int head[N] , to[N << 1] , len[N << 1] , next[N << 1] , cnt , fa[N] , deep[N] , vis[N] , v[N] , sum[N] , tot , q[N] , l , r;
inline void add(int x , int y , int z)
{
to[++cnt] = y , len[cnt] = z , next[cnt] = head[x] , head[x] = cnt;
}
void dfs(int x)
{
int i;
for(i = head[x] ; i ; i = next[i])
if(to[i] != fa[x])
fa[to[i]] = x , deep[to[i]] = deep[x] + len[i] , dfs(to[i]);
}
void getdis(int x , int now , int p)
{
int i;
v[p] = max(v[p] , now);
for(i = head[x] ; i ; i = next[i])
if(!vis[to[i]])
vis[to[i]] = 1 , getdis(to[i] , now + len[i] , p);
}
int main()
{
int n , m , i , x , y , z , mx , p = 0 , ans = 1 << 30;
scanf("%d%d" , &n , &m);
for(i = 1 ; i < n ; i ++ ) scanf("%d%d%d" , &x , &y , &z) , add(x , y , z) , add(y , x , z);
dfs(1) , mx = -1;
for(i = 1 ; i <= n ; i ++ )
if(deep[i] > mx)
x = i , mx = deep[i];
fa[x] = deep[x] = 0 , dfs(x) , mx = -1;
for(i = 1 ; i <= n ; i ++ )
if(deep[i] > mx)
y = i , mx = deep[i];
for(i = y ; i ; i = fa[i]) vis[i] = 1;
for(i = y ; i ; i = fa[i]) getdis(i , 0 , ++tot) , sum[tot + 1] = sum[tot] + deep[i] - deep[fa[i]];
for(i = 1 ; i <= tot ; i ++ )
{
while(p <= tot && sum[p + 1] - sum[i] <= m)
{
p ++ ;
while(l <= r && v[q[r]] <= v[p]) r -- ;
q[++r] = p;
}
ans = min(ans , max(max(sum[i] , sum[tot] - sum[p]) , v[q[l]]));
if(q[l] <= i) l ++ ;
}
printf("%d
" , ans);
return 0;
}