【bzoj4555】[Tjoi2016&Heoi2016]求和 NTT

题目描述

在2016年，佳媛姐姐刚刚学习了第二类斯特林数，非常开心。

现在他想计算这样一个函数的值:

S(i, j)表示第二类斯特林数，递推公式为:

S(i, j) = j ∗ S(i − 1, j) + S(i − 1, j − 1), 1 <= j <= i − 1。

边界条件为：S(i, i) = 1(0 <= i), S(i, 0) = 0(1 <= i)

你能帮帮他吗?

输入

输入只有一个正整数

输出

 输出f(n)。由于结果会很大，输出f(n)对998244353(7 × 17 × 223 + 1)取模的结果即可。1 ≤ n ≤ 100000

样例输入

3

---

题解

NTT

考虑第二类斯特林数的公式：

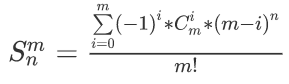
（第二类斯特林数的含义是把n个数分成m个非空集合的方案数，考虑容斥，如果不考虑集合的无序性，至少有i个空集的方案数为$C_m^i*(m-i)^n$，除以$m!$后容斥一下，故有此式）

然后答案就是：

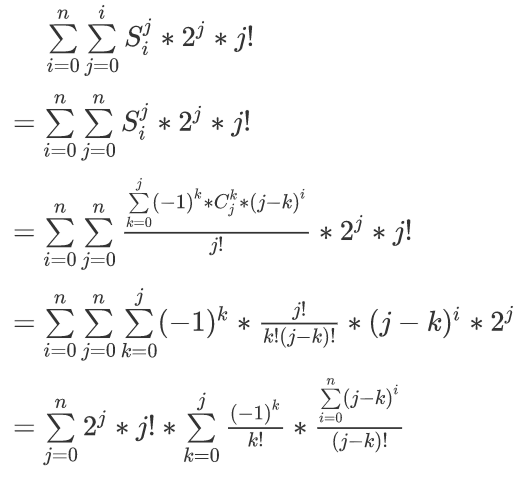
很容易发现后面的$sum$是一个卷积的形式，设$f(x)=frac{(-1)^x}{x!},g(x)=frac{sumlimits_{i=0}^nx^i}{x!}$，那么答案为$sumlimits_{j=0}^nh(j)=sumlimits_{j=0}^nf*g(j)$。

使用NTT加速求解，时间复杂度为$O(nlog n)$。

注意当首项为1时，等比数列求和公式不能使用，需要特判。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 300010
using namespace std;
typedef long long ll;
const ll mod = 998244353;
ll fac[N] , p[N] , a[N] , b[N];
ll pow(ll x , ll y)
{
	ll ans = 1;
	while(y)
	{
		if(y & 1) ans = ans * x % mod;
		x = x * x % mod , y >>= 1;
	}
	return ans;
}
void ntt(ll *a , int len , int flag)
{
	int i , j , k;
	for(i = k = 0 ; i < len ; i ++ )
	{
		if(i > k) swap(a[i] , a[k]);
		for(j = len >> 1 ; (k ^= j) < j ; j >>= 1);
	}
	for(k = 2 ; k <= len ; k <<= 1)
	{
		ll wn = pow(3 , (mod - 1) / k);
		if(flag == -1) wn = pow(wn , mod - 2);
		for(i = 0 ; i < len ; i += k)
		{
			ll w = 1 , t;
			for(j = i ; j < i + (k >> 1) ; j ++ , w = w * wn % mod)
				t = w * a[j + (k >> 1)] % mod , a[j + (k >> 1)] = (a[j] - t + mod) % mod , a[j] = (a[j] + t) % mod;
		}
	}
	if(flag == -1)
	{
		k = pow(len , mod - 2);
		for(i = 0 ; i < len ; i ++ ) a[i] = a[i] * k % mod;
	}
}
int main()
{
	int n , i , len = 1;
	ll inv = 1 , ans = 0;
	scanf("%d" , &n);
	a[0] = b[0] = fac[0] = p[0] = 1;
	for(i = 1 ; i <= n ; i ++ )
	{
		fac[i] = fac[i - 1] * i % mod , p[i] = p[i - 1] * 2 % mod;
		inv = inv * pow(i , mod - 2) % mod;
		if(i & 1) a[i] = mod - inv;
		else a[i] = inv;
		if(i == 1) b[i] = n + 1;
		else b[i] = (pow(i , n + 1) - 1) * (pow(i - 1 , mod - 2)) % mod * inv % mod;
	}
	while(len <= 2 * n) len <<= 1;
	ntt(a , len , 1) , ntt(b , len , 1);
	for(i = 0 ; i < len ; i ++ ) a[i] = a[i] * b[i] % mod;
	ntt(a , len , -1);
	for(i = 0 ; i <= n ; i ++ ) ans = (ans + fac[i] * p[i] % mod * a[i]) % mod;
	printf("%lld
" , ans);
	return 0;
}