2021.7.14模拟赛
比赛概括:
(mathrm{sum}=0+2.5+60+0)
唉。
T1 树的直径:
题目大意:
每次询问一个叶子节点,它会产生两个儿子,并求出整个树的当前直径。
思路:
有一个性质:当前直径的某一点必是上一直径的某端点。
那么离线把树构造出来,每次就用 LCA 比大小即可。
代码:
const int N = 2e5 + 10;
inline ll Read()
{
ll x = 0, f = 1;
char c = getchar();
while (c != '-' && (c < '0' || c > '9')) c = getchar();
if (c == '-') f = -f, c = getchar();
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
return x * f;
}
int m, s, t, n, logN;
struct edge
{
int to, nxt;
}e[N << 1];
int head[N], tot;
void add(int u, int v)
{
e[++tot] = (edge) {v, head[u]}, head[u] = tot;
}
bool vis[N];
int dep[N], f[N][30];
queue <int> q;
void bfs(int root)
{
while(!q.empty()) q.pop();
q.push(root);
vis[root] = 1;
while (!q.empty())
{
int u = q.front(); q.pop();
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (vis[v]) continue;
vis[v] = 1;
dep[v] = dep[u] + 1;
f[v][0] = u;
for (int j = 1; j <= logN; j++)
f[v][j] = f[f[v][j-1]][j - 1];
q.push(v);
}
}
}
int LCA(int u, int v)
{
if (dep[u] > dep[v]) u ^= v ^= u ^= v;
for (int j = logN; ~j; j--)
if (dep[f[v][j]] >= dep[u])
v = f[v][j];
if (u == v) return u;
for (int j = logN; ~j; j--)
if (f[u][j] != f[v][j])
u = f[u][j], v = f[v][j];
u = f[u][0];
return u;
}
int ques[N], ans = 2;
int main()
{
m = Read();
add(1, 2), add(2, 1), add(1, 3), add(3, 1), add(1, 4), add(4, 1);
n = 4;
for (int i = 1; i <= m; i++)
{
int u = Read();
add(++n, u), add(u, n);
add(++n, u), add(u, n);
ques[i] = n;
}
logN = log2(n) + 1;
s = 2, t = 3;
bfs(1);
for (int i = 1; i <= m; i++)
{
int c = LCA(s, ques[i]),
ans1 = dep[s] + dep[ques[i]] - 2 * dep[c];
c = LCA(t, ques[i]);
int ans2 = dep[t] + dep[ques[i]] - 2 * dep[c];
if (ans1 > ans && ans1 >= ans2) ans = ans1, t = ques[i];
if (ans2 > ans && ans2 > ans1) ans = ans2, s = ques[i];
printf ("%d
", ans);
}
return 0;
}
T2 积木:
题目大意:
在一个全为零的数列中,每次可以选择一段数字相同的区间 ([l,r]),使得 ([l+1,r-1]) 变为原区间的数加一。
现在给你一段不全的数列,问你构造方案数。
思路:
把其看作是网格图:

可以往右上、右下、正右方向走,每次求 (a) 点到 (b) 点的方案,并且不能超过 (0) 线。
若没有 (0) 线,可以枚举正右的次数 (d),并可以直接求出向上、向下各走多少次。则有答案:(C_{len}^{d} imes C_{len-d}^{up})。
而有 (0) 线则可以通过容斥减去越过之的方案数,转化为:
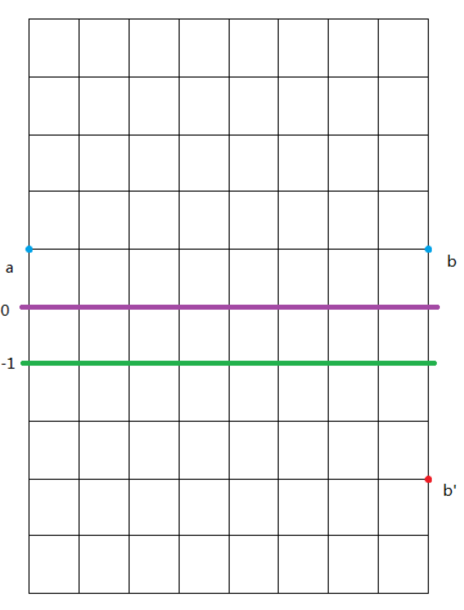
即从 (a) 到 (b')。方法与上面一样,详见代码。
代码:
const int N = 2e5 + 10;
inline ll Read()
{
ll x = 0, f = 1;
char c = getchar();
while (c != '-' && (c < '0' || c > '9')) c = getchar();
if (c == '-') f = -f, c = getchar();
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
return x * f;
}
int n;
int a[N];
int ans = 1;
int mod = 1e9 + 7;
int qpow(int a, int b)
{
int ans = 1;
for (; b; a = 1ll * a * a % mod, b >>= 1)
if (b & 1) ans = 1ll * a * ans % mod;
return ans;
}
int fac[N << 2], ifac[N << 2];
int C(int n, int m)
{
return 1ll * fac[n] * ifac[m] % mod * 1ll * ifac[n - m] % mod;
}
int main()
{
freopen("brick.in", "r", stdin);
freopen("brick.out", "w", stdout);
n = Read();
fac[0] = 1;
for (int i = 1; i <= 4 * n; i++)
fac[i] = 1ll * fac[i - 1] * i % mod;
ifac[n * 4] = qpow(fac[n * 4], mod - 2);
for (int i = 4 * n; i; i--)
ifac[i - 1] = 1ll * ifac[i] * i % mod;
int l, r; l = 1;
for (r = 1; r <= n; a[r] > -1? l = r: 0, r++)
{
a[r] = Read();
if (r == 1 || r == n)
{
if (a[r] == -1) a[r] = 0;
else if (a[r]) {puts("0"); return 0;}
}
if (a[r] == -1 || r == 1) continue;
if (abs(a[r] - a[l]) > r - l) {puts("0"); return 0;}
int len = r - l, dif = a[r] - a[l], dif2 = -a[l] - a[r] - 2;
int tmp = 0;
for (int d = 0; d <= len - abs(dif); d++)
{
int up, down;
if ((len - d + dif) % 2 || len - d + dif < 0) continue;
up = (len - d + dif) / 2;
down = (len - d + dif2) / 2;
(tmp += 1ll * C(len, d) * ((1ll * C(len - d, up) + mod - C(len - d, down)) % mod) % mod) %= mod;
}
ans = 1ll * ans * tmp % mod;
}
printf ("%d", ans);
return 0;
}
T3 软件公司:
题目大意:
一家软件开发公司有两个项目,并且这两个项目都由相同数量的m个子项目组成,对于同一个项目,每个子项目都是相互独立且工作量相当的,并且一个项目必须在m个子项目全部完成后才算整个项目完成。
这家公司有n名程序员分配给这两个项目,每个子项目必须由一名程序员一次完成,多名程序员可以同时做同一个项目中的不同子项目。
求最小的时间T使得公司能在T时间内完成两个项目。
正文:
很容易想到设 (f_{i,j,k}) 表示前 (i) 个人做了 (j) 次项目一、(k) 次项目二的最短时间。则有:
时间复杂度 (mathcal{O}(nm^4))。
式子中包含最大值最小,以此为突破口二分时间,那么设 (f_{i,j,k}) 表示前 (i) 个人做了 (j) 次项目一、(k) 次项目二能否在规定时间完成。时间复杂度 (mathcal{O}(nm^3log10000))。
再优化,发现状态可以改设为 (f_{i,j}) 表示前 (i) 个人做 (j) 次项目一的情况下最多能做多少项目二。则有:
其中的 (mathrm{mid}) 表示二分的时间。时间复杂度 (mathcal{O}(nm^2log10000))。
代码:
const int N = 210;
inline ll Read()
{
ll x = 0, f = 1;
char c = getchar();
while (c != '-' && (c < '0' || c > '9')) c = getchar();
if (c == '-') f = -f, c = getchar();
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
return x * f;
}
int n, m;
int a[N], b[N], f[N][N];
int ans;
bool check(int x)
{
memset (f, -127 / 3, sizeof f);
f[0][0] = 0;
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= j; k++)
if(x - k * a[i] < 0) break;
else f[i][j] = max(f[i][j], f[i - 1][j - k] + (x - k * a[i]) / b[i]);
return f[n][m] >= m;
}
int main()
{
freopen("company.in", "r", stdin);
freopen("company.out", "w", stdout);
n = Read(), m = Read();
for (int i = 1; i <= n; i++)
a[i] = Read(), b[i] = Read();
int l = 1, r = 10000, mid;
while (l <= r)
{
mid = l + r >> 1;
if (check(mid)) ans = mid, r = mid - 1;
else l = mid + 1;
}
printf ("%d
", ans);
return 0;
}
T4 我图呢:
题目大意:

正文:
经过仔细阅读发现题意是在二分图上找最大权值最大独立集。源点向二分图第一部分或第二部分向汇点都连一条容量是点权的边,第一部分向第二部分连无穷的边。跑 dinic 后,在残余网络上找合法方案。
代码:
const int M = 100010, N = 310;
inline ll Read()
{
ll x = 0, f = 1;
char c = getchar();
while (c != '-' && (c < '0' || c > '9')) c = getchar();
if (c == '-') f = -f, c = getchar();
while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
return x * f;
}
int n, m, s, t, tot;
ll w[N];
struct edge
{
int y; ll w;int op, next;
} e[M];
int head[N];
void Add(int x, int y, ll w)
{
e[++tot] = (edge){y, w, tot + 1, head[x]};
head[x] = tot;
e[++tot] = (edge){x, 0, tot - 1, head[y]};
head[y] = tot;
}
ll dis[N];
queue <int> que;
bool bfs()
{
while(!que.empty())que.pop();
memset(dis, 127 / 3, sizeof(dis));
dis[s] = 0;
que.push(s);
while(!que.empty())
{
int x = que.front();que.pop();
for (int i = head[x]; i; i = e[i].next)
{
int y = e[i].y;
if(dis[y] >= dis[x] + 1 && e[i].w)
{
dis[y] = dis[x] + 1;
if(y == t) return 1;
que.push(y);
}
}
}
return 0;
}
ll dfs(int x, ll f)
{
if(x == t) return f;
ll sum = 0;
for (int i = head[x]; i; i = e[i].next)
{
int y = e[i].y;
if(dis[y] == dis[x] + 1 && e[i].w)
{
ll f2 = dfs(y, min(e[i].w * 1ll, f - sum));
if (!f2) dis[y] = -1;
e[i].w -= f2;
e[e[i].op].w += f2;
sum += f2;
if (sum == f) break;
}
}
return sum;
}
ll dinic()
{
ll sum = 0;
while(bfs()){sum += dfs(s, 1e20);}
return sum;
}
bool isPart2[N];
namespace OldEdge
{
struct edge
{
int from, to, nxt;
} e[M];
int head[N], tot;
void add(int x, int y)
{
e[++tot] = (edge){x, y, head[x]}, head[x] = tot;
}
bool vis[N];
void dfs(int u, bool part)
{
vis[u] = 1;
if (part)
Add(s, u, 1e9 + w[u]);
else isPart2[u] = 1, Add(u, t, 1e9 + w[u]);
for (int i = head[u], v; i; i = e[i].nxt)
if (!vis[v = e[i].to]) dfs(v, part ^ 1);
}
void Prework(int m)
{
for (int i = 1; i <= m; i++)
{
int u = Read(), v = Read();
add(u, v), add(v, u);
}
for (int i = 1; i <= n; i++)
if (!vis[i]) dfs(i, 1);
for (int i = 1; i <= 2 * m; i += 2)
{
int u = e[i].from, v = e[i].to;
if (isPart2[u]) u ^= v ^= u ^= v;
Add(u, v, 1e10), Add(v, u, 0);
}
}
}
bool vis[N];
void dfs(int u)
{
vis[u] = 1;
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].y;
if(!vis[v] && e[i].w > 0) dfs(v);
}
}
int main()
{
freopen("graph.in", "r", stdin);
freopen("graph.out", "w", stdout);
scanf("%d%d", &n, &m);
s = n + 1, t = n + 2;
for (int i = 1; i <= n; i++)
w[i] = Read();
OldEdge::Prework(m);
dinic();
dfs(s);
int ans1, ans2; ans1 = ans2 = 0;
for (int i = 1; i <= n; i++)
if (isPart2[i] ^ vis[i]) ans1 ++, ans2 += w[i];
printf ("%d %d
", ans1, ans2);
for (int i = 1; i <= n; i++)
printf ("%d", isPart2[i] ^ vis[i]);
return 0;
}