消息传递
链接:
题目大意:
一个点在某一秒可向相邻节点扩散,问哪些节点开始扩散能最快多少秒将所有节点全部覆盖。
思路:
先想暴力,对于每个点求出 (f_i) 表示从以 (i) 为根的子树中扩散到 (i),最长花费的时间。则有:
[f_u=max_{vinmathrm{son}(x)}{f_v+mathrm{order}_v}
]
其中 (mathrm{order}_v) 表示 (u) 扩散到 (v) 的顺序,可以贪心排序求出。然后每个点都作为根算一遍,时间复杂度 (mathcal{O}(n^2log n))。
但是如果暴力算法,很多状态都重复算了:

如图,两个灰点作根,与深灰点的 (f_i) 无关。
则设 (g_i) 表示从以 (i) 为根的子树外扩散到 (i),最长花费的时间:
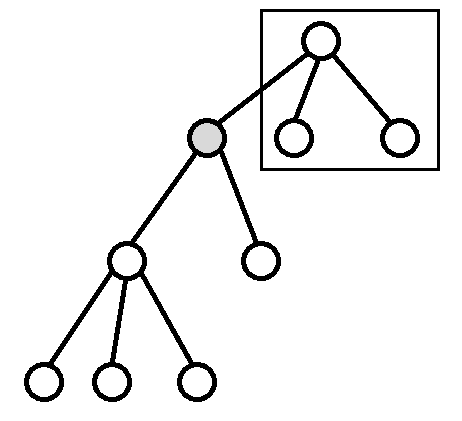
如图,黑框内则表示为灰点的 (g_i)。则有:
[g_u=max_{k=mathrm{fa}(x)}(g_k+mathrm{order}_k,max_{vinmathrm{son}(k),v
e u}{f_v+mathrm{order}_v})
]
实现时建议由当前节点推出子节点的 (g_i)。
统计答案时就在排 (mathrm{order}_i) 时顺便找到最大的即可。