感谢 @一个低调的人 (UID=48417)
题目:

思路:
这是一个一眼题
我们不妨把所有的数都看做是(1)(取相应的花费,如:(6) 的花费就是(6 - 1 = 5), 拿变量(ans)记录)。
如果这一个是负数,拿一个变量(negative)记录负数的数量。
对于负数,当有偶数个的时候,把他们都变成(-1)是无所谓的,因为偶数个(-1)相乘的最终答案是(1),所以当有偶数个负数时答案为(ans - negative imes 2)(乘上(2)是因为(1)变成(-1)要两步)。
但当有奇数个的时候,我们肯定选(negative-1)个负数改成(-1),不然最后乘积就是(-1)了。
所以最终答案是(ans - [(negative - negative ~ mod ~ 2) imes 2])
嗯~我们充满信心地交到评测姬上评测:

嗯????(我头像)
真是奇怪。为啥会WA?
在我百思不得其解时,dalao告诉我我错误原因——有(0)的情况。
当我们有奇数个负数,当有(0)时,把所有负数都可以变为(-1)!
因为(0)它变(1)还是变(-1),都是花费(1)块钱。因此,有奇数个负数并且有(0)时,就先把(ans-2)再作偶数个负数的情况。
举个栗子(请大家自行手玩):
0 5 -3 -6 -9
我们原来的答案是:
[egin{matrix}ans - [(negative - negative ~ mod ~ 2) imes 2]\ =26-[(3-3~mod~2) imes 2]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\ =26-4~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\ =22~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~end{matrix}
]
但实际上应该是(20)
(请仔细阅读完再看代码)
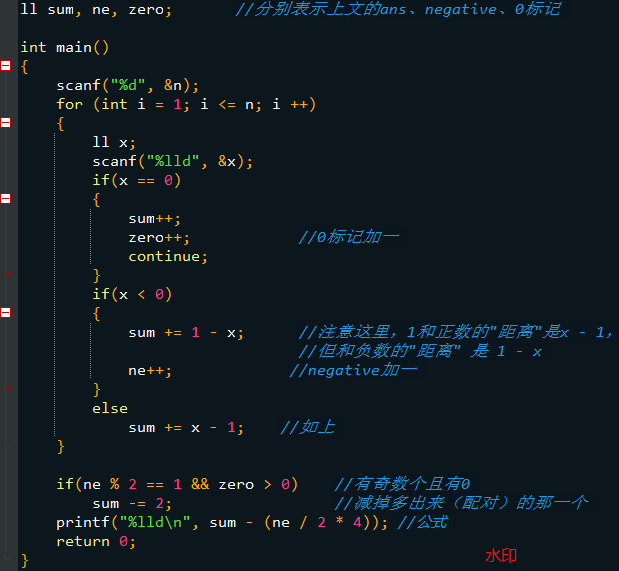
AC代码: