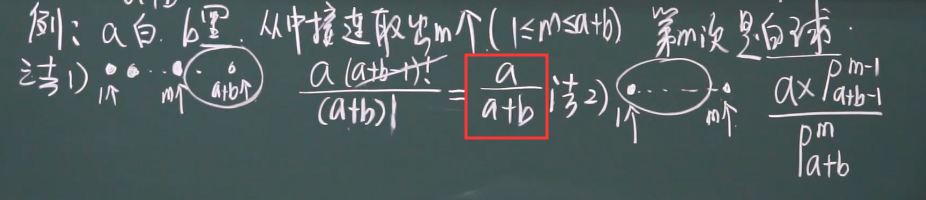1. 事件的基本概率
- (P(A)): 表示为事件A的概率.
- (P(Omega) = 1)
- (P(emptyset)=0)
- (0leq P(A) leq 1)
2. 古典概率模型(排列组合)理论
古典概率模型条件:
- 有限个样本点
- 等可能性(每一个样本点出现的概率一样)
[P(A)=frac{A的样本点总数}{Omega的样本点数}=frac{A中包含的基本事件}{Omega基本事件总数}
]
排列组合概念
排列(Permutation)
从m个不同元素中挑出n个不同的元素,所有不同排列的个数称为排列数.
- 排列可分选排列与全排列两种,
- (P_m^n): 当(n<m)时,成为排列,当(m=n)时,成为全排列
[P_n^m=frac{n!}{(n-m)!}=n(n-1)(n-2)cdotcdotcdotcdot(n-m+1)
]
- 注: (0!=1)
组合(Combination)
从m个不同元素中挑出n个不同的元素,所有不同组合的个数称为组合数.
即用其排列再除以其重复的组合数
[C_n^m=frac{A_n^m}{n!}=frac{n!}{m(n-m)!}
]
[C_n^m=frac{A_n^m}{m!}
]
[C_n^0=C_n^n=1
]
[C_n^m=C_n^{n-m}=1
]
3. 例题