容斥原理

容斥原理两种表示

当需要求一些集合的并集时需要用到容斥原理

1. 用韦恩图表示容斥原理
   
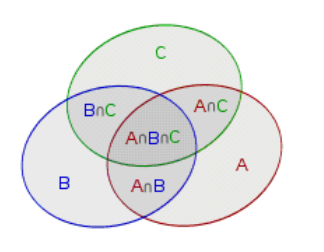
   (S(i))：集合i中元素个数
   (S(A cup B cup C) = S(A) + S(B) + S(C) - S(A cap B) - S(A cap C) - S(B cap C) + S(A cap B cap C))
2. 用公式表示容斥原理
   其中的||表示集合中元素个数
   (|A_1 cup A_2 cup ... A_m| = displaystylesum_{1 leq i leq m}|A_i| - displaystylesum_{1 leq i < j leq m}|A_i cap A_j| + displaystylesum_{1 leq i < j < k leq m}|A_i cap A_j cap A_k| - ... + (-1)^{m - 1}|A_1 cap A_2 cap ... cap A_m|)

应用

能被整除的数

给定一个整数n和m个不同的质数(p_1,p_2,…,p_m)。请你求出1~n中能被(p_1,p_2,…,p_m)中的至少一个数整除的整数有多少个。

题目分析

解决本题还需要使用倍数和二进制状态压缩的相关知识，但这里我们主要想要讨论的是容斥原理的应用，所以这两部分的内容在此不再进行阐述。
将一个质数的倍数看为一个集合，不同质数可能会有相同倍数，体现在图形上也就是两个集合间存在交集，恰好就是韦恩图的样式，我们要计算的就是这些集合的交集，所以我们按照容斥原理的公式求解即可，代码实现上难点在于两方面：1.如何枚举所有集合的交集。2. 如何快速计算出两个集合交集中元素的数量
解决方法对应着上面提到的两个知识：1. 二进制状态压缩 2.如何快速计算倍数个数

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 20;

int n, m;
int p[N];

int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; ++ i) cin >> p[i];
    
    int res = 0;
    // 二进制状态压缩
    for (int i = 1; i < (1 << m); ++ i) // 遍历所有情况，二进制中1的数量代表集合中质数的个数
    {
        int x = 1, cnt = 0; // x : 此时质数的乘积 cnt: 此时质数的个数用于确定正负
        for (int j = 0; j < m; ++ j)
            if (i >> j & 1)
            {
                if ((LL)x * p[j] > n)
                {
                    x = -1;
                    break;
                }
                ++ cnt;
                x *= p[j];   
            }
        
        if (x != -1)
        {
            // 求倍数的个数
            if (cnt % 2) res += n / x;
            else res -= n / x;
        }
    }
    
    cout << res << endl;
    return 0;
}