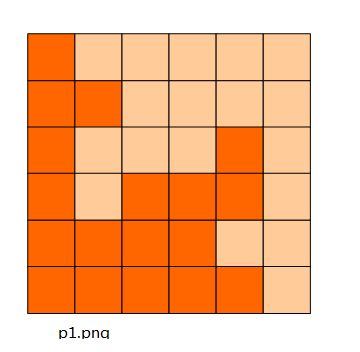
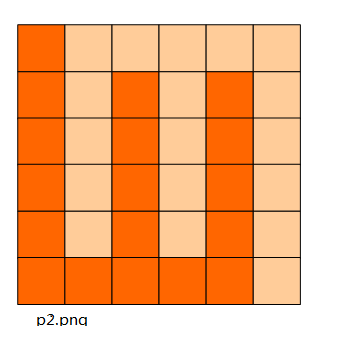
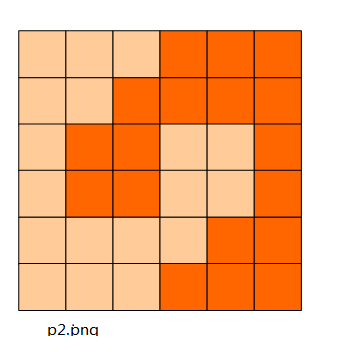
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
代码来自这里,看了好久大佬的代码才看懂,代码是抄的,注释是自己写的,不知道写错没有
#include<bits/stdc++.h>
using namespace std;
int book[10][10];
int dire[4][2]={-1,0,1,0,0,-1,0,1};//这种顺序是保证每次移动都是平行移动(不存在对角线那种移动)
const int N=6;
int ans;
void dfs(int x,int y)
{
if(x==0||y==N||x==N||y==0)//到达正方形的边缘
{
ans++;
return;
}//一次涂色完成,情况数+1
for(int i=0;i<4;i++)
{
int nx=x+dire[i][0];
int ny=y+dire[i][1];//移动
if(nx<0||nx>N||y<0||ny>N) continue;//跑到正方形外
if(book[nx][ny]==0)//如果没有涂色
{
book[nx][ny]=1;
book[N-nx][N-ny]=1;//标记涂色部分
dfs(nx,ny);//以nx,ny为起点继续涂色(标记)
book[nx][ny]=0;
book[N-nx][N-ny]=0;//一次涂色完成后把标记的涂色部分清空
}
}
}
int main()
{
book[N/2][N/2]=1;
dfs(N/2,N/2);
cout<<ans/4<<endl;
return 0;
}