求逆元的方法及模板

数论倒数，又称逆元，在数论中很有意义。在数论中取模运算十分普遍，我们知道取模运算有如下性质：

(a +  b) % p = (a%p +  b%p) %p  （对）

(a  -  b) % p = (a%p  -  b%p + p) %p  （对）

(a  *  b) % p = (a%p *  b%p) %p  （对）

(a  /  b) % p = (a%p  /  b%p) %p  （错）

对除法操作来说，就无法直接进行取模运算了，那么应该怎样做呢，就需要用到逆元了。若a*x=1(mod p)，其中gcd(a,p)=1，即a，p互质，则称x为a关于p的逆元，或者a,x关于p互为逆元。称a的逆元为inv(a)，这样就将除法取模运算转换成(a/b)%p=(a*inv(b))%p=(a%p*inv(b)%p)%p。

逆元怎么求：

方法一——费马小定理求逆元：

（前提是p为质数，否则不能用）根据费马小定理，当gcd(a,p)=1时，有a^(p-1)=1 (mod p)，即a*a^(p-2)=1 (mod p)，即a关于p的逆元为a^(p-2)，用快速幂即可求。

模板：

LL pow_mod(LL a, LL b, LL p){//a的b次方求余p 
    LL ret = 1;
    while(b){
        if(b & 1) ret = (ret * a) % p;
        a = (a * a) % p;
        b >>= 1;
    }
    return ret;
}
LL Fermat(LL a, LL p){//费马求a关于b的逆元 
        return pow_mod(a, p-2, p);
}

方法二——扩展欧基里德求逆元：

若gcd(a,b)=1，则a*x+b*y=1有解，其解的x即为a关于b的逆元，y为b关于a的逆元。

　　证明：a*x+b*y=1  ->   a*x%b+b*y%b=1%b  ->  a*x%b=1%b  ->  a*x=1 (mod b)，即x为a关于b的逆元，同理可证y。

模板：

#include<cstdio>
typedef long long LL;
void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
    if (!b) {d = a, x = 1, y = 0;}
    else{
        ex_gcd(b, a % b, y, x, d);
        y -= x * (a / b);
    }
}
LL inv(LL t, LL p){//如果不存在，返回-1 
    LL d, x, y;
    ex_gcd(t, p, x, y, d);
    return d == 1 ? (x % p + p) % p : -1;
}
int main(){
    LL a, p;
    while(~scanf("%lld%lld", &a, &p)){
        printf("%lld
", inv(a, p));
    }
}

方法三：

一个常见的问题：已知b|a(b能整除a)，求a/b mod m，我们发现费马小定理和扩展欧基里德求逆元都有局限，需要gcd(a,p)=1。实际上还有一种通用的求逆元的方法，适合所有情况。即a/b % m=a%(b*m)/b。证明：

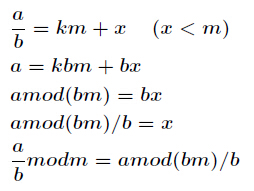
方法四：

（前提为p是质数，否则不能用）inv(a) = (p - p / a) * inv(p % a) % p，然后一直递归到1即可，因为1的逆元是1。

　　证明：
　　　　设x = p % a,y = p / a
　　　　于是有 x + y * a = p
　　　　(x + y * a) % p = 0
　　　　移项得 x % p = (-y) * a % p
　　　　x * inv(a) % p = (-y) % p
　　　　inv(a) = (p - y) * inv(x) % p
　　　　于是 inv(a) = (p - p / a) * inv(p % a) % p

这个方法不限于求单个逆元，比前两个好，它可以在O(n)的复杂度内算出n个数的逆元。

模板：

#include<cstdio>
typedef long long LL;
LL inv(LL t, LL p) {//求t关于p的逆元，注意:t要小于p，最好传参前先把t%p一下 
    return t == 1 ? 1 : (p - p / t) * inv(p % t, p) % p;
}
int main(){
    LL a, p;
    while(~scanf("%lld%lld", &a, &p)){
        printf("%lld
", inv(a%p, p));
    }
}