5436.一维数组的动态和
给你一个数组 nums 。数组「动态和」的计算公式为:runningSum[i] = sum(nums[0]…nums[i]) 。
请返回 nums 的动态和。
样例输入与样例输出 Sample Input and Sample Output
示例 1:
**输入:** nums = [1,2,3,4]
**输出:** [1,3,6,10]
**解释:** 动态和计算过程为 [1, 1+2, 1+2+3, 1+2+3+4] 。
示例 2:
**输入:** nums = [1,1,1,1,1]
**输出:** [1,2,3,4,5]
**解释:** 动态和计算过程为 [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1] 。
示例 3:
**输入:** nums = [3,1,2,10,1]
**输出:** [3,4,6,16,17]
提示 Hint
提示:
1 <= nums.length <= 1000-10^6 <= nums[i] <= 10^6
题解
class Solution {
public:
vector<int> runningSum(vector<int>& nums) {
const int n = nums.size();
int s(0);
vector<int>ans(n);
for(int i = 0; i < n; ++i)
ans[i] += s += nums[i];
return ans;
}
};
5437.不同整数的最少数目
给你一个整数数组 arr 和一个整数 k 。现需要从数组中恰好移除 k 个元素,请找出移除后数组中不同整数的最少数目。
样例输入与样例输出 Sample Input and Sample Output
示例 1:
**输入:** arr = [5,5,4], k = 1
**输出:** 1
**解释:** 移除 1 个 4 ,数组中只剩下 5 一种整数。
示例 2:
**输入:** arr = [4,3,1,1,3,3,2], k = 3
**输出:** 2
**解释:** 先移除 4、2 ,然后再移除两个 1 中的任意 1 个或者三个 3 中的任意 1 个,最后剩下 1 和 3 两种整数。
提示 Hint
提示:
1 <= arr.length <= 10^51 <= arr[i] <= 10^90 <= k <= arr.length
题解
class Solution {
public:
int findLeastNumOfUniqueInts(vector<int>& arr, int k) {
map<int, int>g;
for(int i : arr)
g[i]++;
vector<pair<int, int>>p;
for(pair<int, int>i : g)
p.push_back(make_pair(i.second, i.first));
sort(p.begin(), p.end());
int ans(p.size());
for(int i = 0; i < p.size(); ++i) {
if(k >= p[i].first)
k -= p[i].first;
else
return p.size() - i;
}
return 0;
}
};
5438.制作 m 束花所需的最少天数
给你一个整数数组 bloomDay,以及两个整数 m 和 k 。
现需要制作 m 束花。制作花束时,需要使用花园中 相邻的k 朵花 。
花园中有 n 朵花,第 i 朵花会在 bloomDay[i] 时盛开, 恰好 可以用于 一束 花中。
请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1 。
样例输入与样例输出 Sample Input and Sample Output
示例 1:
**输入:** bloomDay = [1,10,3,10,2], m = 3, k = 1
**输出:** 3
**解释:** 让我们一起观察这三天的花开过程,x 表示花开,而 _ 表示花还未开。
现在需要制作 3 束花,每束只需要 1 朵。
1 天后:[x, _, _, _, _] // 只能制作 1 束花
2 天后:[x, _, _, _, x] // 只能制作 2 束花
3 天后:[x, _, x, _, x] // 可以制作 3 束花,答案为 3
示例 2:
**输入:** bloomDay = [1,10,3,10,2], m = 3, k = 2
**输出:** -1
**解释:** 要制作 3 束花,每束需要 2 朵花,也就是一共需要 6 朵花。而花园中只有 5 朵花,无法满足制作要求,返回 -1 。
示例 3:
**输入:** bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3
**输出:** 12
**解释:** 要制作 2 束花,每束需要 3 朵。
花园在 7 天后和 12 天后的情况如下:
7 天后:[x, x, x, x, _, x, x]
可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花,因为它们不相邻。
12 天后:[x, x, x, x, x, x, x]
显然,我们可以用不同的方式制作两束花。
示例 4:
**输入:** bloomDay = [1000000000,1000000000], m = 1, k = 1
**输出:** 1000000000
**解释:** 需要等 1000000000 天才能采到花来制作花束
示例 5:
**输入:** bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2
**输出:** 9
提示 Hint
提示:
bloomDay.length == n1 <= n <= 10^51 <= bloomDay[i] <= 10^91 <= m <= 10^61 <= k <= n
题解
class Solution {
public:
int gao(vector<int>&bloomDay, int k, int x) {
int ans(0);
for(int i = 0, p = 0; i < bloomDay.size(); i++) {
if(bloomDay[i] <= x)
p++;
else
p = 0;
if(p == k)
p = 0, ans++;
}
return ans;
}
int minDays(vector<int>& bloomDay, int m, int k) {
if(m * k > bloomDay.size())
return -1;
set<int>a_s;
for(int i : bloomDay)
a_s.insert(i);
vector<int>a(a_s.begin(), a_s.end());
int first = 0, len = a.size();
int half, mid;
while(len > 0) {
half = len >> 1;
mid = first + half;
if(gao(bloomDay, k, a[mid]) < m) {
first = mid + 1;
len = len - half - 1;
} else
len = half;
}
return a[first];
}
};
5188.树节点的第 K 个祖先
给你一棵树,树上有 n 个节点,按从 0 到 n-1 编号。树以父节点数组的形式给出,其中 parent[i] 是节点 i
的父节点。树的根节点是编号为 0 的节点。
请你设计并实现 getKthAncestor``(int node, int k) 函数,函数返回节点 node 的第 k
个祖先节点。如果不存在这样的祖先节点,返回 -1 。
树节点的第 _k _个祖先节点是从该节点到根节点路径上的第 k 个节点。
示例:
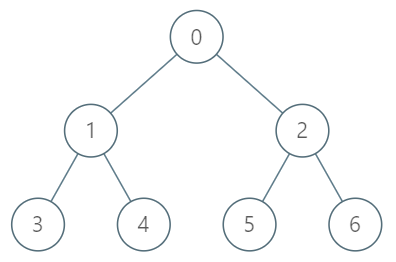
**输入:**
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]
**输出:**
[null,1,0,-1]
**解释:**
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // 返回 1 ,它是 3 的父节点
treeAncestor.getKthAncestor(5, 2); // 返回 0 ,它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3); // 返回 -1 因为不存在满足要求的祖先节点
提示 Hint
提示:
1 <= k <= n <= 5*10^4parent[0] == -1表示编号为0的节点是根节点。- 对于所有的
0 < i < n,0 <= parent[i] < n总成立 0 <= node < n- 至多查询
5*10^4次
题解
class TreeAncestor {
public:
vector<vector<int>>g;
vector<int>dep;
vector<vector<int>>f;
TreeAncestor(int n, vector<int>& parent) {
g = vector<vector<int>>(n);
dep = vector<int>(n);
f = vector<vector<int>>(n, vector<int>(16, -1));
for(int u = 0; u < n; ++u) {
int v = parent[u];
if(v == -1)
continue;
//g[u].push_back(v);
g[v].push_back(u);
}
dep[0] = 1;
DFS(0, -1);
}
void DFS(int u, int fa) {
if(fa >= 0)
dep[u] = dep[fa] + 1;
f[u][0] = fa;
for(int i = 1; i < 16; i++)
f[u][i] = f[u][i - 1] != -1 ? f[f[u][i - 1]][i - 1] : -1;
for(int v : g[u]) {
if(v != fa)
DFS(v, u);
}
}
int getKthAncestor(int x, int k) {
int t = dep[x] - k;
if(t <= 0)
return -1;
for(int i = 16 - 1; i >= 0; i--) {
if(f[x][i] != -1 && dep[f[x][i]] > t)
x = f[x][i];
}
return f[x][0];
}
};
/**
* Your TreeAncestor object will be instantiated and called as such:
* TreeAncestor* obj = new TreeAncestor(n, parent);
* int param_1 = obj->getKthAncestor(node,k);
*/