一些闲话:旅行传送门
A. Busiest Computing Nodes
题意:给你一个含有 \(k\) 个节点,编号从 \(0\) 至 \(k-1\) 的计算集群,以及一组已知到达时间与处理时间的请求(亦从 \(0\) 开始编号)。
当每个请求到达时,它会优先进入第 (\(i\) % \(k\)) 个节点,若当前节点正忙,则根据开放定址法去找下一个空闲节点(如果最终都没能找到空闲的节点,该请求将被忽略)。
现在问你在发送完这组请求后,哪些节点处理的请求数量最多?
题目分析:显然,请求的结束时间(即节点可以被重新启用的时间)= 到达时间 + 处理时间。
先考虑暴力的做法,新请求到来时扫一遍当前节点,如果有节点满足条件(节点内请求的结束时间 \(\leq\) 当前请求的到达时间)就进行更新,时间复杂度约为 \(O(nk)\) ,必 \(T\)。
这里采取线段树+二分查询优化,时间复杂度 \(O(nlogk)\) ,具体看图:
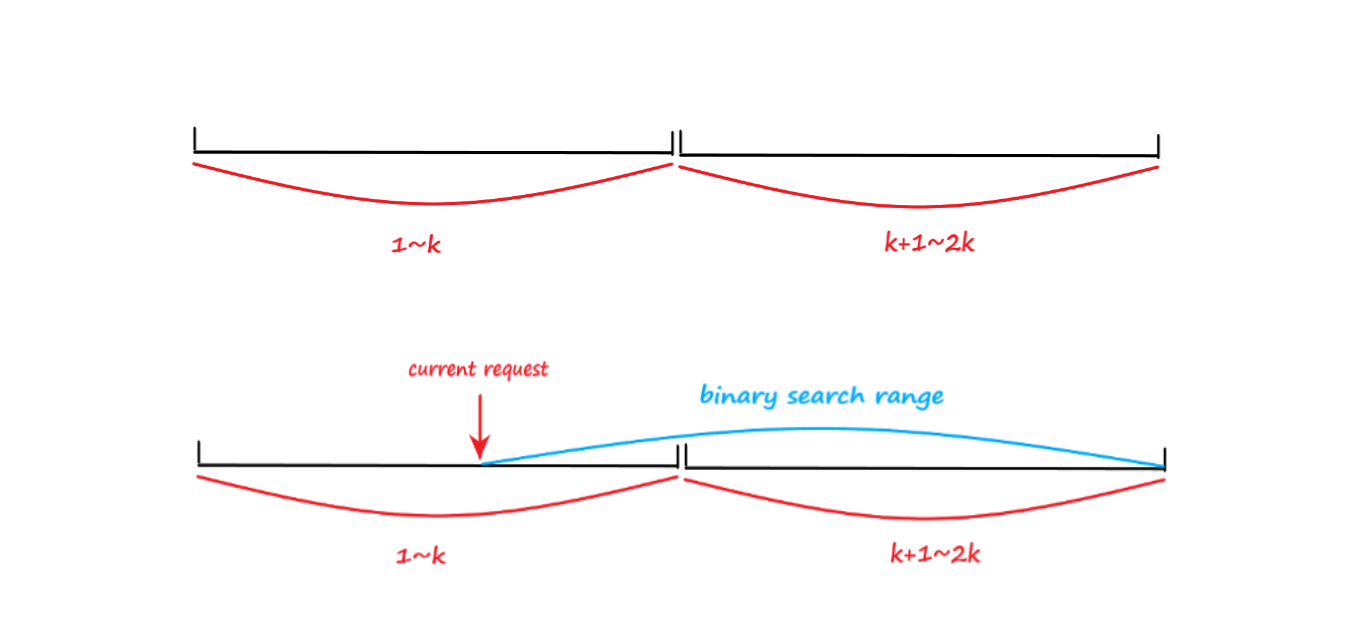
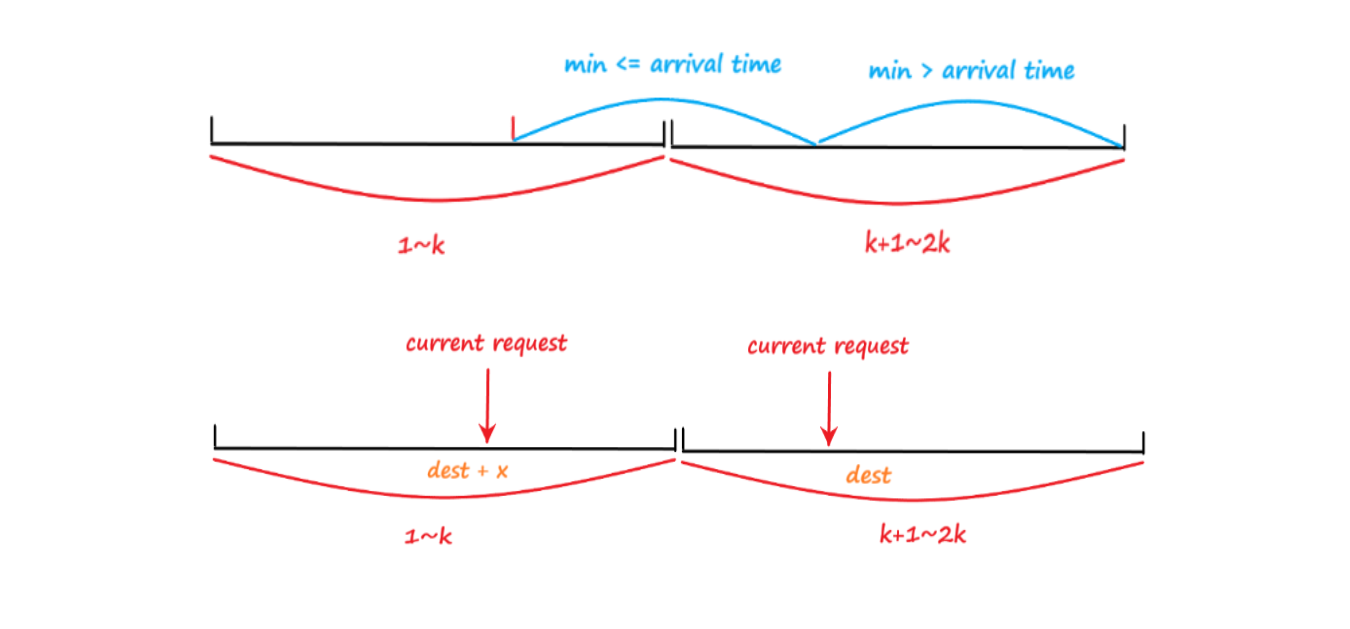
- 线段树维护区间最小值,单点修改,区间查询
- 根据最小值进行二分,为了方便查询我拷贝了一份节点(也可以先查 \(i\) ~ \(k-1\) ,再查 \(0\) ~ \(i-1\) ),更新时同时更新两个就好。
- 注意输出格式,行尾无空格(白 PE 六发,真的傻逼)
AC代码:
#include <bits/stdc++.h>
using ll = long long;
using namespace std;
const int maxn = 2e5 + 10;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline ll read()
{
ll x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
ll k, n, ans[maxn];
struct obj
{
ll idx, ar, pro;
} a[maxn];
#define lson k << 1
#define rson k << 1 | 1
struct node
{
int s, t;
ll mn;
} tree[maxn << 2];
void pushup(int k) { tree[k].mn = min(tree[lson].mn, tree[rson].mn); }
void build(int k, int s, int t)
{
tree[k].s = s, tree[k].t = t;
if (s == t)
return;
int mid = (s + t) >> 1;
build(lson, s, mid);
build(rson, mid + 1, t);
pushup(k);
}
void update(int k, int p, ll x)
{
if (tree[k].s == tree[k].t && tree[k].s == p)
{
tree[k].mn = x;
return;
}
int mid = (tree[k].s + tree[k].t) >> 1;
p <= mid ? update(lson, p, x) : update(rson, p, x);
pushup(k);
}
ll query(int k, int s, int t)
{
if (s <= tree[k].s && tree[k].t <= t)
return tree[k].mn;
int mid = (tree[k].s + tree[k].t) >> 1;
if (t <= mid)
return query(lson, s, t);
else if (s > mid)
return query(rson, s, t);
else
return min(query(lson, s, mid), query(rson, mid + 1, t));
}
int main()
{
k = read(), n = read();
for (int i = 1; i <= n; i++)
a[i].ar = read(), a[i].pro = read(), a[i].idx = i - 1;
build(1, 1, 2 * k);
for (int i = 1; i <= n; i++)
{
ll st = a[i].idx % k + 1, ed = st + k - 1;
int l = st, r = ed;
while (l < r)
{
int mid = (l + r) >> 1;
if (query(1, l, mid) <= a[i].ar)
r = mid;
else
l = mid + 1;
}
ll dest = l;
if (query(1, dest, dest) <= a[i].ar)
{
update(1, dest, a[i].ar + a[i].pro);
if (dest <= k)
update(1, dest + k, a[i].ar + a[i].pro), ans[dest - 1]++;
else
update(1, dest - k, a[i].ar + a[i].pro), ans[dest - k - 1]++;
}
}
ll mx = 0;
for (int i = 0; i < k; i++)
mx = max(mx, ans[i]);
vector<int> realans;
for (int i = 0; i < k; i++)
if (ans[i] == mx)
realans.push_back(i);
for (int i = 0; i < realans.size() - 1; i++)
printf("%d ", realans[i]);
printf("%d", realans[realans.size() - 1]);
return 0;
}
D. Edge of Taixuan
题意:给你 \(n\) 个点和 \(m\) 次操作,每次操作令区间 \([l, r]\) 中的点两两相连构成一张边权为 \(w\) 的完全图,求要得到最小生成树所需删除边的边权总和。
题目分析:将所有操作按边权降序排序,接下来按区间覆盖问题来做就好,最终得到的最小生成树一定是一条链,答案即为总边权减去最小生成树的权重,线段树与分块均可,分块要跑得快一些。
AC代码(线段树):
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
using ll = long long;
const ll inf = 1e10;
const int maxn = 5e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
struct cable
{
int l, r, w;
bool operator<(const cable &lhs) const { return lhs.w < w; }
} q[maxn];
#define lson k << 1
#define rson k << 1 | 1
struct node
{
int l, r, flag;
ll sum, tag;
} tree[maxn << 2];
void pushup(int k)
{
if (tree[lson].flag && tree[rson].flag)
tree[k].flag = 1;
tree[k].sum = tree[lson].sum + tree[rson].sum;
}
void pushdown(int k)
{
ll v = tree[k].tag;
tree[lson].sum = (tree[lson].r - tree[lson].l + 1) * v;
tree[rson].sum = (tree[rson].r - tree[rson].l + 1) * v;
tree[lson].tag = tree[rson].tag = v;
tree[k].tag = 0;
}
void build(int k, int l, int r)
{
tree[k].l = l, tree[k].r = r;
tree[k].sum = inf, tree[k].tag = tree[k].flag = 0;
if (l == r)
return;
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
}
void update(int k, int l, int r, int x)
{
if (l <= tree[k].l && tree[k].r <= r)
{
tree[k].sum = (tree[k].r - tree[k].l + 1) * x;
tree[k].tag = x;
tree[k].flag = 1;
return;
}
if (tree[k].tag)
pushdown(k);
int mid = (tree[k].l + tree[k].r) >> 1;
if (r <= mid)
update(lson, l, r, x);
else if (l > mid)
update(rson, l, r, x);
else
update(lson, l, mid, x), update(rson, mid + 1, r, x);
pushup(k);
}
void solve()
{
ll ans = 0;
int n = read() - 1, m = read();
build(1, 1, n);
rep(i, 1, m)
{
q[i].l = read(), q[i].r = read(), q[i].w = read();
ans += 1ll * (q[i].r - q[i].l + 1) * (q[i].r - q[i].l) / 2 * q[i].w;
}
std::sort(q + 1, q + m + 1);
rep(i, 1, m) update(1, q[i].l, q[i].r - 1, q[i].w);
if (!tree[1].flag)
puts("Gotta prepare a lesson");
else
printf("%lld\n", ans - tree[1].sum);
}
int main(int argc, char const *argv[])
{
int T = read();
rep(cas, 1, T)
{
printf("Case #%d: ", cas);
solve();
}
return 0;
}
AC代码(分块):
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
using ll = long long;
const ll inf = 1e10;
const int maxn = 5e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int n, m, block, num, l[maxn], r[maxn], bel[maxn];
ll tag[maxn], a[maxn];
struct cable
{
int l, r, w;
bool operator<(const cable &rhs) const { return w > rhs.w; }
} q[maxn];
void build()
{
rep(i, 1, n) a[i] = tag[i] = inf;
block = sqrt(n), num = (n - 1) / block + 1;
rep(i, 1, n) bel[i] = (i - 1) / block + 1;
rep(i, 1, num) l[i] = (i - 1) * block + 1, r[i] = i * block;
r[num] = n;
}
void update(int ql, int qr, int c)
{
int bl = bel[ql], br = bel[qr];
rep(i, ql, std::min(qr, r[bl])) a[i] = c;
if (bl ^ br)
{
rep(i, bl + 1, br - 1) tag[i] = c;
rep(i, l[br], qr) a[i] = c;
}
}
void solve()
{
ll ans = 0, sum = 0;
n = read() - 1, m = read();
build();
rep(i, 1, m)
{
q[i].l = read(), q[i].r = read(), q[i].w = read();
ans += 1ll * (q[i].r - q[i].l + 1) * (q[i].r - q[i].l) / 2 * q[i].w;
}
std::sort(q + 1, q + m + 1);
rep(i, 1, m) update(q[i].l, q[i].r - 1, q[i].w);
rep(i, 1, n) sum += std::min(a[i], tag[bel[i]]);
if (sum >= inf)
puts("Gotta prepare a lesson");
else
printf("%lld\n", ans - sum);
}
int main(int argc, char const *argv[])
{
int T = read();
rep(cas, 1, T)
{
printf("Case #%d: ", cas);
solve();
}
return 0;
}
F. Land Overseer
题意:给你两个圆心分别为 \((a,b)\) 与 \((2a,0)\) 的圆 \(A\) 、 \(B\) ,半径均为 \(r\) 的圆,现从原点出发,问先经过圆 \(A\) 再经过圆 \(B\) 的最短路径是多少?
题目分析:分两种情况讨论,具体看图和代码:
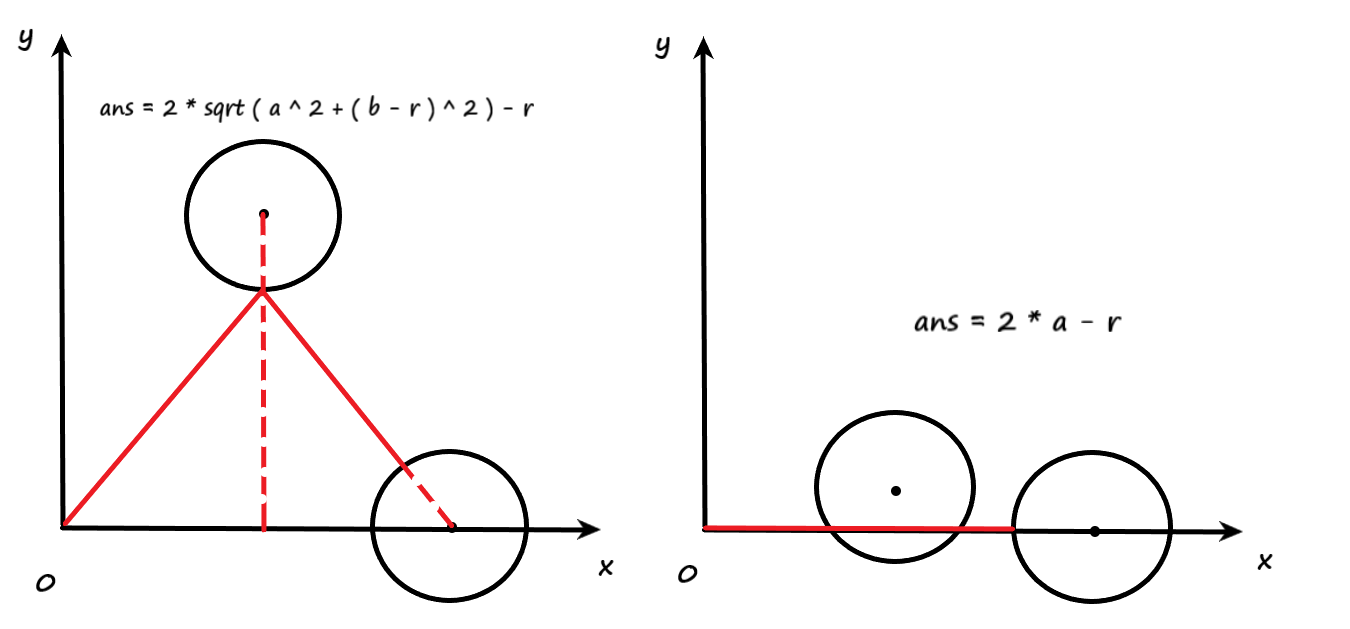
AC代码:
#include <bits/stdc++.h>
using ll = long long;
using namespace std;
int T;
ll a, b, R;
int main()
{
scanf("%d", &T);
for (int i = 1; i <= T; i++)
{
scanf("%lld%lld%lld", &a, &b, &R);
double ans = 0;
if (a > R && b <= R)
ans = 2.0 * a - 1.0 * R;
else
ans = 2.0 * sqrt(a * a + (b - R) * (b - R)) - 1.0 * R;
printf("Case #%d: %.2lf\n", i, ans);
}
return 0;
}
H. Mesh Analysis
题意:给你 \(n\) 个点的坐标,这些点构成了一些三角形和线段。每次询问一个点所有的邻点与所在图形的编号。
题目分析:最开始 \(cx\) 理解的意思就是对的,我也想过坐标是不是没用,但可惜没能猜透出题人的心思,往复杂的方面去想了,赛后交流的时候发现有几支队伍也想歪了,大家都在考虑怎么判断某个点包不包含在其它三角形内,一致认为这是个几何题,各种叉乘去搞。
结果笑死,哪有我们想的这么高大上,用 \(map\) 直接记录就完事了。md搁着猜谜呢,和出题人心意不相通还写不了题了。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
#define IOS \
ios::sync_with_stdio(false); \
cin.tie(nullptr); \
cout.tie(nullptr)
using db = double;
using namespace std;
map<int, set<int>> mp1;
map<int, set<int>> mp2;
int main(int argc, char const *argv[])
{
IOS;
int n, m;
cin >> n >> m;
int id, type;
db x, y, z;
rep(i, 1, n) cin >> id >> x >> y >> z;
rep(i, 1, m)
{
cin >> id >> type;
if (type == 203)
{
cin >> x >> y >> z;
mp1[x].insert(y), mp1[x].insert(z);
mp1[y].insert(x), mp1[y].insert(z);
mp1[z].insert(x), mp1[z].insert(y);
mp2[x].insert(id), mp2[y].insert(id), mp2[z].insert(id);
}
else
{
cin >> x >> y;
mp1[x].insert(y), mp1[y].insert(x);
mp2[x].insert(id), mp2[y].insert(id);
}
}
int q;
cin >> q;
rep(i, 1, q)
{
cin >> id;
cout << id << endl;
cout << "[";
for (auto it : mp1[id])
{
if (it ^ *mp1[id].begin())
cout << ",";
cout << it;
}
cout << "]" << endl;
cout << "[";
for (auto it : mp2[id])
{
if (it ^ *mp2[id].begin())
cout << ",";
cout << it;
}
cout << "]";
if (i ^ q)
cout << "" << endl;
}
return 0;
}
I. Neighborhood Search
题意:给你一个序列 \(S\) 和一个数 \(A\) ,找出序列中所有与 \(A\) 的差值 \(\leq r\) 的元素,降序输出。
题目分析:签到题,降序排列后 \(O(n)\) 扫一遍就好,难点主要在处理输入数据上。
AC代码:
#include <bits/stdc++.h>
using ll = long long;
using namespace std;
const int maxn = 1e5 + 10;
ll s[maxn], len, ans;
int main()
{
while (scanf("%lld", &s[++len]) != EOF)
;
len -= 3;
sort(s + 1, s + len + 1, greater<ll>());
ll a = s[len + 1], r = s[len + 2];
for (int i = 1; i <= len; i++)
if (abs(s[i] - a) <= r)
printf("%lld ", s[i]), ++ans;
if (!ans)
printf("\n");
return 0;
}
J. Red-Black Paths
题意:给你一张初始全为白点的空图,按照时间顺序建图,建图过程中会将白点染成红黑色,求相邻两次询问间新增的红黑路(红点到黑点)的路径长的异或和,红黑路的路径长指的是路径上每个点的编号乘以当前长度的总和。
题目分析:离线算法,记录每个操作当前的时间戳。先 \(dfs\) 标记所有能到达黑点的点,然后构造新图,只把有用的边连上,再对每个红点进行 \(dfs\) 计算其构成的每条红黑路的路径长,根据之前记录的时间戳来更新答案以保证正确性。最后维护个前缀异或和,对每个询问输出 \(ans_{q[i]} \bigoplus ans_{q[i-1]}\) 即可。
AC代码:
#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
#define pii std::pair<int, int>
#define mp std::make_pair
const int maxn = 2e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int n, m, col[maxn], T[maxn], vis[maxn], tag[maxn], ans[maxn];
struct edge
{
int u, v, t;
};
std::vector<int> red, q;
std::vector<pii> g[maxn];
std::vector<edge> e;
void dfs1(int u)
{
vis[u] = 1;
if (col[u] == 2)
tag[u] = 1;
for (auto x : g[u])
{
int v = x.first;
if (!vis[v])
dfs1(v);
tag[u] |= tag[v];
}
}
void dfs2(int u, int len, int sum, int t)
{
sum += u * len++;
if (col[u] == 2)
ans[std::max(T[u], t)] ^= sum;
for (auto x : g[u])
dfs2(x.first, len, sum, std::max(x.second, t));
}
int main(int argc, char const *argv[])
{
m = read();
int op, u, v;
q.push_back(0);
rep(i, 1, m)
{
op = read();
switch (op)
{
case 1:
u = read(), v = read(), n = std::max({n, u, v});
g[u].push_back(mp(v, i)), e.push_back(edge{u, v, i});
break;
case 2:
u = read(), red.push_back(u);
col[u] = 1, T[u] = i;
break;
case 3:
u = read();
col[u] = 2, T[u] = i;
break;
default:
q.push_back(i);
break;
}
}
rep(i, 1, n) if (!vis[i]) dfs1(i);
rep(i, 1, n) g[i].clear();
for (auto x : e)
if (tag[x.u] && tag[x.v])
g[x.u].push_back(mp(x.v, x.t));
for (auto x : red)
dfs2(x, 1, 0, T[x]);
rep(i, 1, m) ans[i] ^= ans[i - 1];
rep(i, 1, q.size() - 1) printf("%d\n", ans[q[i]] ^ ans[q[i - 1]]);
return 0;
}
K. Segment Routing
题意:模拟题,给你一张有向图,每次询问从节点 \(i\) 开始按指定方向走最终到达的点。
题目分析:阅读理解+模拟,跟着题意来就好,越界就判定丢包。
AC代码:
#include <bits/stdc++.h>
using ll = long long;
const int maxn = 1e5 + 5;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
std::vector<int> e[maxn];
int main()
{
int T = read();
for (int cas = 1; cas <= T; cas++)
{
printf("Case #%d: \n", cas);
int n = read(), m = read();
for (int i = 1; i <= n; i++)
e[i].clear();
for (int i = 1; i <= n; i++)
{
int d = read();
for (int j = 1; j <= d; j++)
{
int v = read();
e[i].push_back(v);
}
}
for (int i = 1; i <= m; i++)
{
int u = read(), l = read();
int flag = 1;
for (int j = 1; j <= l; j++)
{
int v = read();
if (!flag)
continue;
if (e[u].size() < v)
{
puts("Packet Loss");
flag = 0;
continue;
}
u = e[u][v - 1];
}
if (flag)
printf("%d\n", u);
}
}
return 0;
}