简介
定义:在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
性质:1. 本身首先是一棵二叉搜索树。
2. 带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
平衡因子:树中任意节点的左子树高度和右子树高度 之差
平衡因子 = | 左子树高度 - 右子树高度 |
AVL树中的任意一个结点, 其平衡因子的绝对值小于2,AVL树是一种特殊的二叉搜索树 (BST树)。
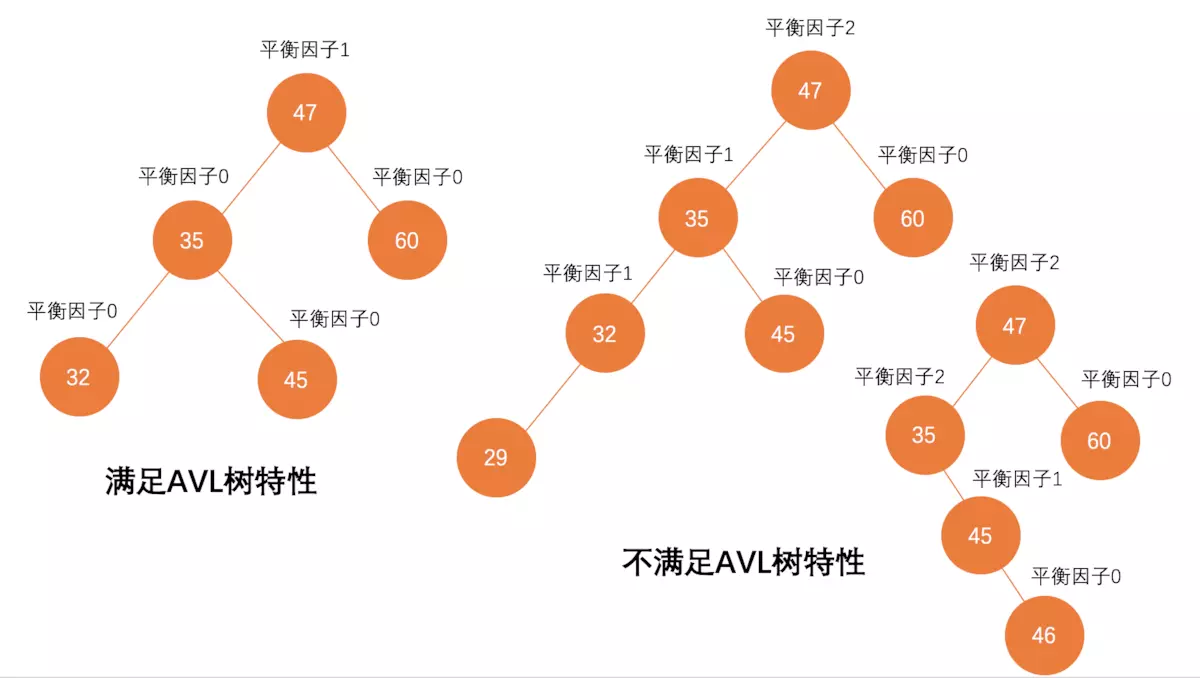
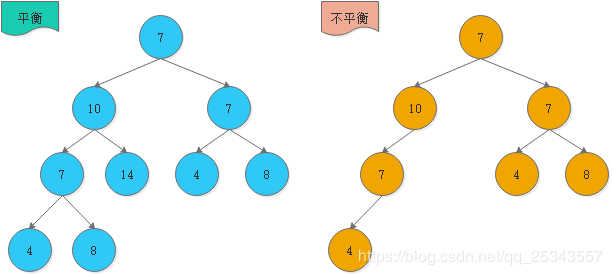
在一些情况下,会打破AVL树的自平衡性,或者在添加删除时打破了平衡性。所以 AVL树定义了旋转操作, 在平衡因子大于等于2时, AVL树会旋转来调整树的结构, 来重新满足平衡因子小于2。
失去平衡后进行进行的规律可归纳为下列四种情况:
(一)单向右旋转处理LL:由于在A的左子树根结点的左子树上插入结点,A的平衡因子由1增至2,致使以A为根的子树失去平衡,则需进行一次右旋转操作;
(二)单向左旋平衡处理RR:由于在A的右子树根结点的右子树上插入结点,A的平衡因子由-1变为-2,致使以A为根的子树失去平衡,则需进行一次左旋转操作;
(三)双向旋转(先左后右)平衡处理LR:由于在A的左子树根结点的右子树上插入结点,A的平衡因子由1增至2,致使以A为根的子树失去平衡,则需进行两次旋转(先左旋后右旋)操作。
图形演示
(一)右旋LL
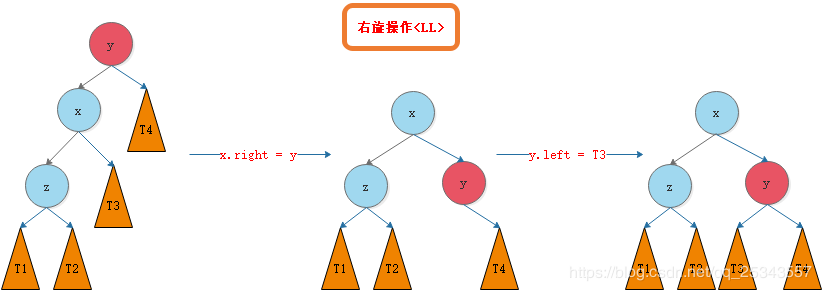
如最后一张图所示。假设T类的节点高度为h,则最开始y的左子树的深度是h+2, y的右子树T4的深度是h, y的平衡因子是2,不符合AVL树的特性,这就不平衡了。平衡因子的绝对值小于等于1才行。所以进行右旋转操作。
右旋转之后,如图可见,x的左右子树的高度都是h+1,所以x的平衡因子是0,满足AVL树的特性,这样就平衡了。
(二)左旋RR
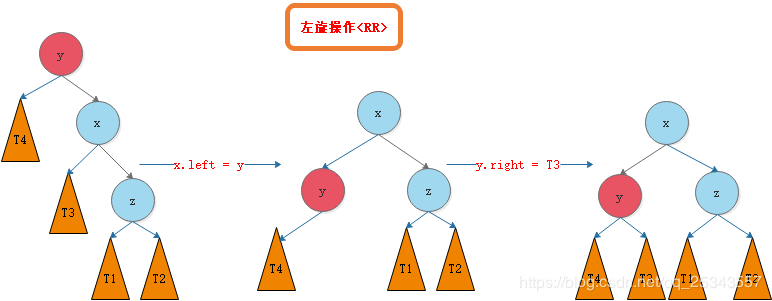
如最后一张图所示。假设T类的节点高度为h,则最开始y的右子树的深度是h+2, y的左子树T4的深度是h, y的平衡因子是2,不符合AVL树的特性,这就不平衡了。平衡因子的绝对值小于等于1才行。所以进行左旋转操作。
右旋转之后,如图可见,x的左右子树的高度都是h+1,所以x的平衡因子是0,满足AVL树的特性,这样就平衡了。
(三)先左后右LR

如图所示。假设T类高度为h, 则y的左子树深度为h+2,右子树深度为h,平衡因子为2,则不平衡。先将x进行左旋转,转化为LL的情况,然后再将y节点进行右旋转,得到AVL平衡树。
(四)先右后左RL
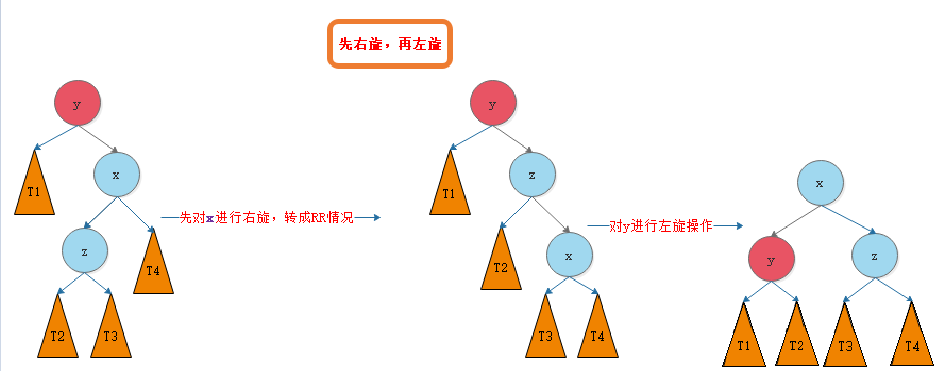
如图所示。假设T类高度为h, 则y的右子树深度为h+2,左子树深度为h,平衡因子为2,则不平衡。先将x进行右旋转,转化为RR的情况,然后再将y节点进行左旋转,得到AVL平衡树。
代码实现
AVL树也是一种二分搜索树,所以我们基于二分搜索树进行增删查改操作。
基础设计
/**
* AVLTree是BST,所以节点值必须是可比较的
*/
public class AvlTree<E extends Comparable<E>>{
private class Node{
public E e;
public Node left;
public Node right;
public int height;
public Node(E e){
this.e = e;
this.left = null;
this.right = null;
this.height = 1;
}
}
private Node root;
private int size;
public AvlTree(){
root=null;
size=0;
}
//获取某一结点的高度
private int getHeight(Node node){
if(node==null){
return 0;
}
return node.height;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
/**
* 获取节点的平衡因子
* @param node
* @return
*/
private int getBalanceFactor(Node node){
if(node==null){
return 0;
}
return getHeight(node.left)-getHeight(node.right);
}
//判断树是否为平衡二叉树
public boolean isBalanced(){
return isBalanced(root);
}
private boolean isBalanced(Node node){
if(node==null){
return true;
}
int balanceFactory = Math.abs(getBalanceFactor(node));//获得平衡因子
if(balanceFactory>1){ //判断平衡因子是否符合
return false;
}
return isBalanced(node.left)&&isBalanced(node.right);//当前节点符合平衡要求,则查看左右子树是否平衡
}
}
我们可以想到,在添加/删除节点的时候,可能会打破平衡。所以打破平衡时,判断是哪一种情况,进行旋转操作。
(A)右旋转操作
// 对节点y进行向右旋转操作,返回旋转后新的根节点x // y x // / / // x T4 向右旋转 (y) z y // / - - - - - - - -> / / // z T3 T1 T2 T3 T4 // / // T1 T2 private Node rightRotate(Node y){ Node x = y.left; Node T3 = x.right; //向右旋转过程 x.right = y; y.left = T3; //更新height y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;//获取左右子树最大高度 加上 自身高度1 x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;//获取左右子树最大高度 加上 自身高度1
return x;
}
(B)左旋转操作
/// 对节点y进行向左旋转操作,返回旋转后新的根节点x
// y x
// / /
// T1 x 向左旋转 (y) y z
// / - - - - - - - -> / /
// T2 z T1 T2 T3 T4
// /
// T3 T4
private Node leftRotate(Node y){
Node x = y.right;
Node T2 = x.left;
//向右旋转过程
x.left = y;
y.right = T2;
//更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
添加操作
// 向二分搜索树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
//更新高度。
node.height = 1 + Math.max(getHeight(node.left),getHeight(node.right));
//计算平衡因子
int balanceFactor = getBalanceFactor(node);
//平衡维护
//LL.左子树-右子树 > 1 && 左子树的左子树深度 大于 左子树的右子树深度
if (balanceFactor >= 1 && getBalanceFactor(node.left) >= 0){
return rightRotate(node);
}
//RR. 左子树 - 右子树 < -1 && 右子树的左子树深度 小于 右子树的右子树深度
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0){
return leftRotate(node);
}
//LR. 左子树 - 右子树 > 1 && 左子树的左子树深度 小于 左子树的右子树深度
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0){
node.left = leftRotate(node.left); //将左旋转得到的子树 设为 当前节点的左子树 形成LL的情况进行右旋转。
return rightRotate(node);
}
//RL. 左子树 - 右子树 < -1 && 右子树的左子树深度 大于 右子树的右子树深度
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0){
node.right = rightRotate(node.right); //将右旋转得到的子树 设为 当前节点的右子树 形成RR的情况进行左旋转
return leftRotate(node);
}
return node;
}
删除操作
public E remove(E e){
Node node = getNode(root, e);
if(node != null){
root = remove(root, e);
return node.value;
}
return null;
}
private Node remove(Node node, E e){
if( node == null )
return null;
Node retNode; //存储删除后的树
if( e.compareTo(node.e) < 0 ){
node.left = remove(node.left , e);
retNode = node;
}
else if(e.compareTo(node.e) > 0 ){
node.right = remove(node.right, e);
retNode = node;
}
else{ // e.compareTo(node.e) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
retNode = rightNode;
}
// 待删除节点右子树为空的情况
else if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
retNode = leftNode;
}else {
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = remove(node.right, successor.e);
successor.left = node.left;
node.left = node.right = null;
retNode = successor;
}
}
if(retNode==null)
return null;
//维护平衡
//更新height
retNode.height = 1+Math.max(getHeight(retNode.left),getHeight(retNode.right));
//计算平衡因子
int balanceFactor = getBalanceFactor(retNode);
//LL.左子树-右子树 > 1 && 左子树的左子树深度 大于 左子树的右子树深度
if(balanceFactor > 1 && getBalanceFactor(retNode.left)>=0) {
return rightRotate(retNode);
}
//RR. 左子树 - 右子树 < -1 && 右子树的左子树深度 小于 右子树的右子树深度
if(balanceFactor < -1 && getBalanceFactor(retNode.right)<=0){
return leftRotate(retNode);
}
//LR. 左子树 - 右子树 > 1 && 左子树的左子树深度 小于 左子树的右子树深度
if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){
node.left = leftRotate(retNode.left); //将左旋转得到的子树 设为 当前节点的左子树 形成LL的情况进行右旋转。
return rightRotate(retNode);
}
//RL. 左子树 - 右子树 < -1 && 右子树的左子树深度 大于 右子树的右子树深度
if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){
node.right = rightRotate(retNode.right); //将右旋转得到的子树 设为 当前节点的右子树 形成RR的情况进行左旋转。
return leftRotate(retNode);
}
return node;
}
主要的核心代码基本完成,主要是在添加删除节点时,会打破AVL树的平衡。通过旋转操作 维持平衡。
总体代码如下:
/** * AVL树 * @param <K> * @param <V> */ public class AVLTree<K extends Comparable<K>, V> { private class Node{ public K key; public V value; public Node left, right; public int height; public Node(K key, V value){ this.key = key; this.value = value; left = null; right = null; height = 1; } } private Node root; private int size; public AVLTree(){ root = null; size = 0; } public int getSize(){ return size; } public boolean isEmpty(){ return size == 0; } //判断该二叉树是否是一颗二分搜索树 public boolean isBST(){ ArrayList<K> keys = new ArrayList<>(); inOrder(root, keys); for (int i = 1; i < keys.size(); i++){ if (keys.get(i-1).compareTo(keys.get(i)) > 0){ return false; } } return true; } private void inOrder(Node node, ArrayList<K> keys){ //中序查询 if (node == null){ return; } inOrder(node.left, keys); keys.add(node.key); inOrder(node.right, keys); } //判断以Node为根的二叉树是否是一颗平衡二叉树,递归算法 public boolean isBalanced(){ return isBalanced(root); } private boolean isBalanced(Node node){ if (node == null){ return true; } int balanceFactor = getBalanceFactor(node); if (Math.abs(balanceFactor) > 1){//判断平衡因子是否大于1,大于1则不是平衡二叉树 return false; } return isBalanced(node.left) && isBalanced(node.right); } //获得节点node的高度值 private int getHeight(Node node){ if (node == null){ return 0; } return node.height; } //获得node节点的平衡因子 private int getBalanceFactor(Node node){ if (node == null) return 0; return getHeight(node.left) - getHeight(node.right); } // 对节点y进行向右旋转操作,返回旋转后新的根节点x // y x // / / // x T4 向右旋转 (y) z y // / - - - - - - - -> / / // z T3 T1 T2 T3 T4 // / // T1 T2 private Node rightRotate(Node y){ Node x = y.left; Node T3 = x.right; //向右旋转过程 x.right = y; y.left = T3; //更新height y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1; x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1; return x; } /// 对节点y进行向左旋转操作,返回旋转后新的根节点x // y x // / / // T1 x 向左旋转 (y) y z // / - - - - - - - -> / / // T2 z T1 T2 T3 T4 // / // T3 T4 private Node leftRotate(Node y){ Node x = y.right; Node T2 = x.left; //向右旋转过程 x.left = y; y.right = T2; //更新height y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1; x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1; return x; } // 向二分搜索树中添加新的元素(key, value) public void add(K key, V value){ root = add(root, key, value); } // 向以node为根的二分搜索树中插入元素(key, value),递归算法 // 返回插入新节点后二分搜索树的根 private Node add(Node node, K key, V value){ if(node == null){ size ++; return new Node(key, value); } if(key.compareTo(node.key) < 0) node.left = add(node.left, key, value); else if(key.compareTo(node.key) > 0) node.right = add(node.right, key, value); else // key.compareTo(node.key) == 0 node.value = value; //更新高度 node.height = 1 + Math.max(getHeight(node.left),getHeight(node.right)); //计算平衡因子 int balanceFactor = getBalanceFactor(node); //平衡维护 //LL if (balanceFactor >= 1 && getBalanceFactor(node.left) >= 0){ return rightRotate(node); } //RR if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0){ return leftRotate(node); } //LR if (balanceFactor > 1 && getBalanceFactor(node.left) < 0){ node.left = leftRotate(node.left); return rightRotate(node); } //RL if (balanceFactor < -1 && getBalanceFactor(node.right) > 0){ node.right = rightRotate(node.right); return leftRotate(node); } return node; } public boolean contains(K key){ return getNode(root, key) != null; } public V get(K key){ Node node = getNode(root, key); return node == null ? null : node.value; } public void set(K key, V newValue){ Node node = getNode(root, key); if(node == null) throw new IllegalArgumentException(key + " doesn't exist!"); node.value = newValue; } // 返回以node为根节点的二分搜索树中,key所在的节点 private Node getNode(Node node, K key){ if(node == null) return null; if(key.equals(node.key)) return node; else if(key.compareTo(node.key) < 0) return getNode(node.left, key); else // if(key.compareTo(node.key) > 0) return getNode(node.right, key); } // 返回以node为根的二分搜索树的最小值所在的节点 private Node minimum(Node node){ if(node.left == null) return node; return minimum(node.left); } // 从二分搜索树中删除键为key的节点 public V remove(K key){ Node node = getNode(root, key); if(node != null){ root = remove(root, key); return node.value; } return null; } private Node remove(Node node, K key){ if( node == null ) return null; Node retNode; if( key.compareTo(node.key) < 0 ){ node.left = remove(node.left , key); retNode = node; } else if(key.compareTo(node.key) > 0 ){ node.right = remove(node.right, key); retNode = node; } else{ // key.compareTo(node.key) == 0 // 待删除节点左子树为空的情况 if(node.left == null){ Node rightNode = node.right; node.right = null; size --; retNode = rightNode; } else if(node.right == null){// 待删除节点右子树为空的情况 Node leftNode = node.left; node.left = null; size --; retNode = leftNode; }else { // 待删除节点左右子树均不为空的情况 // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点 // 用这个节点顶替待删除节点的位置 Node successor = minimum(node.right); successor.right = remove(node.right, successor.key); successor.left = node.left; node.left = node.right = null; retNode = successor; } } if (retNode == null){ return null; } /**删除之后,进行二叉树平衡的调整**/ //更新高度 retNode.height = 1 + Math.max(getHeight(retNode.left),getHeight(retNode.right)); //计算平衡因子 int balanceFactor = getBalanceFactor(retNode); //平衡维护 //LL if (balanceFactor >= 1 && getBalanceFactor(retNode.left) >= 0){ return rightRotate(retNode); } //RR if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){ return leftRotate(retNode); } //LR if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){ node.left = leftRotate(retNode.left); return rightRotate(retNode); } //RL if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){ retNode.right = rightRotate(retNode.right); return leftRotate(retNode); } return retNode; } }