实际上树和图的广度&深度优先遍历方法十分类似,所以今天针对树的遍历方法实现进行详细分析,并且树的遍历在笔试中也是非常常见的一种方法,并且《剑指Offer》中的许多面试题用到了这两种遍历方法进行不同需求的算法实现。
深度优先遍历
深度优先遍历:借助递归算法不断遍历当前遍历到节点的左右子节点,对于树这个数据结构根据左子节点、右子节点和当前节点的遍历顺序该搜索算法又可分为前序、中序和后序遍历,其中中序遍历可以达到排序的效果。
具体的遍历顺序如下图所示:
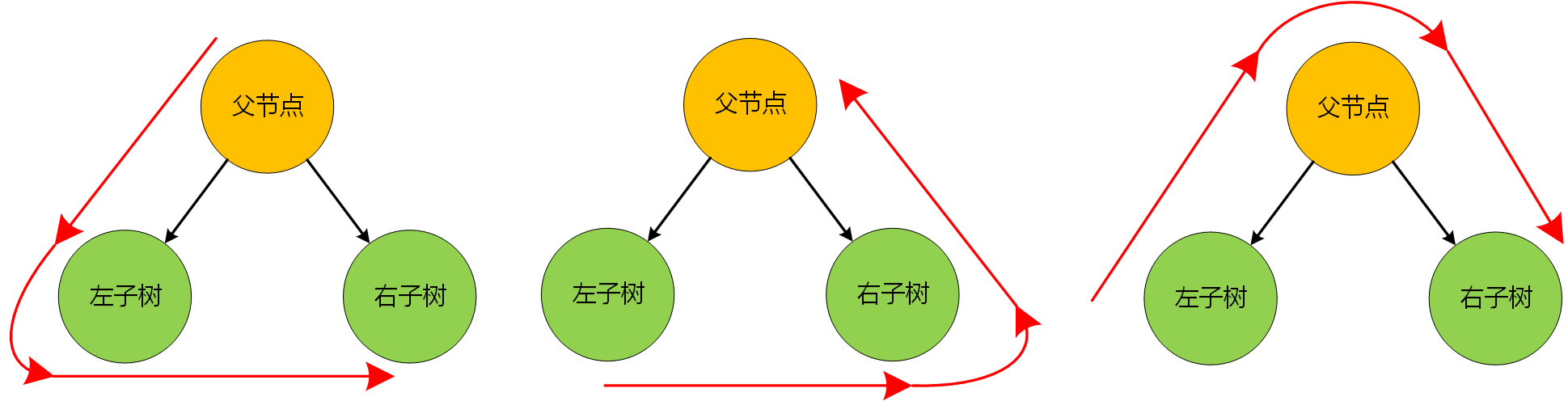
依次为 前序,后序,中序遍历。
代码实现如下:
// 前序遍历
void preOrder() {
preOrder(root);
}
// 对以node为根的二叉搜索树进行前序遍历
void preOrder(Node *node) {
if (node != nullptr) {
std::cout << node->key << " ";
preOrder(node->left);
preOrder(node->right);
}
}
// 中序遍历
void inOrder() {
inOrder(root);
}
// 对以node为根的二叉搜索树进行中序遍历
void inOrder(Node *node) {
if (node != nullptr) {
inOrder(node->left);
std::cout << node->key << " ";
inOrder(node->right);
}
}
// 后序遍历
void postOrder() {
postOrder(root);
}
// 对以node为根的二叉搜索树进行后序遍历
void postOrder(Node *node) {
if (node != nullptr) {
postOrder(node->left);
postOrder(node->right);
std::cout << node->key << " ";
}
}
广度优先搜索
广度优先搜索:实际上就是层序遍历,顾名思义从上到下一层一层的遍历,树的广度优先搜索是借助队列这个数据结构达到层序遍历的效果,及将已遍历的节点的子节点加入队列,并且出队进行遍历,保证了上层数据优先遍历。
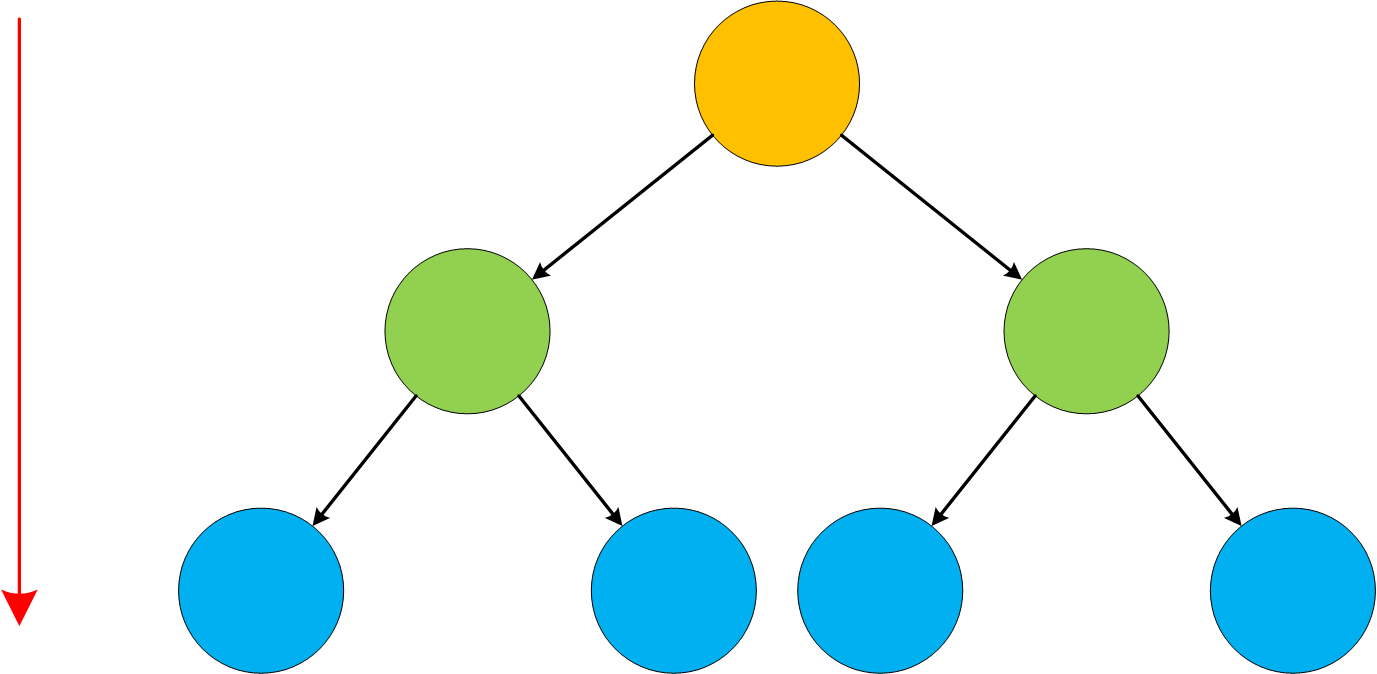
具体的遍历顺序如下图所示,即先遍历黄色节点,再遍历绿色节点,最终遍历蓝色节点。
// 层序遍历
void levelOrder() {
std::queue<Node *> q;
q.push(root);
while (!q.empty()) {
Node *node = q.front();
q.pop();
std::cout << node->key << " ";
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}