[ ext{题目大意}
]
(quad)求从一个点到另一个点所需的距离,相邻两步不能向同一个方向走。
[ ext{思路}
]
(quad)可以发现答案至少是两个点的曼哈顿距离 ,题目的意思是 (x,y) 方向上移动的长度相等或相差 (1),设 (a),(b) 分别表示 (x),(y) 方向上的距离差。
(quad)显然如图,当起点和终点在一条斜线上的时候(即 (abs(a-b)<=1)),此时的答案就是曼哈顿距离,如 ((0,0)->(3,4)=7,(0,0)->(4,4)=8),可以发现沿斜线走是最优的,答案 (ans=a+b)。(没有浪费步数且满足条件)

(quad)当不满足最优情况的时候,显然意味着要浪费步数,我们可以先沿斜线使得在同一条水平线或竖直线上,假设 (a>b+1),然后在沿 (x) 方向的时候,(y) 方向显然就要左右横跳,就是按下图的方式走。
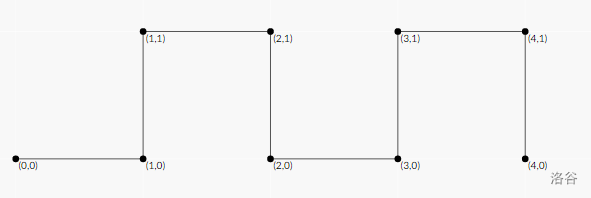
(quad)此时距离为 (abs(a-b)),答案 (ans=min(a,b) imes2+)⌊(abs(a-b)/2)⌋( imes 4+(abs(a-b)mod 2))。
(quad)最后记得开long long。
#include<iostream>
#include<cstdio>
using namespace std;
#define int long long
int q,a,b,c,d;
inline int min(int x,int y){return x<=y?x:y;}
signed main()
{
cin>>q;
while(q--){
cin>>a>>b>>c>>d;
a=abs(a-c);b=abs(b-d);
if(abs(a-b)<=1)printf("%lld",a+b),putchar('
');
else {
int x=abs(a-b);
if(x&1)printf("%lld
",min(a,b)*2+(x-1)*2+1);
else printf("%lld
",min(a,b)*2+x*2);
}
}
return 0;
}