一、CART(分类回归树)
1.思想:
一种采用基尼信息增益作为划分属性的二叉决策树。基尼指数越小,表示纯度越高。
2.回归:
每个节点都有一个预测值,预测值等于属于该节点的所有样例的平均值,分支时,选择每个属性的每个阈值的最好分割点,衡量的标准是最小化均方差。
训练:对训练样本的第i(1<=i<=n)个属性,穷举每个分割点,找到均方差最小的分割点进行分割,该节点的值设为落到该节点的训练样本的平均值,直到不可分或者到一定高度或者属性使用完或者均方差不下降。
测试:对测试样本按照训练时的分割点进行下落,落到叶节点,叶节点的平均值即为预测值。
二、GBDT(梯度提升决策树)
1.原理:
用多棵回归树(或多个弱分类器)进行集成,其中的多棵树不是独立的,而是后面的树在前者的基础上学习误差,所有树的结果加起来是预测得到的结果。弱分类器一般采用CART。
2.过程:
原始回归树:
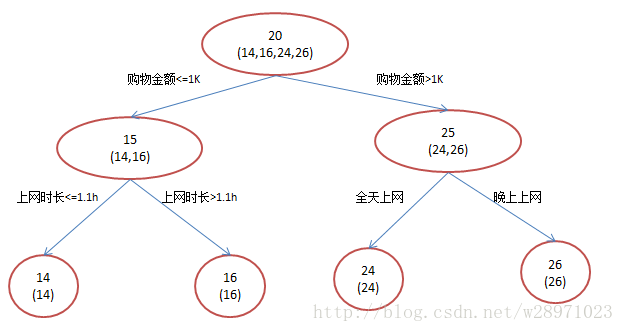
GBDT:
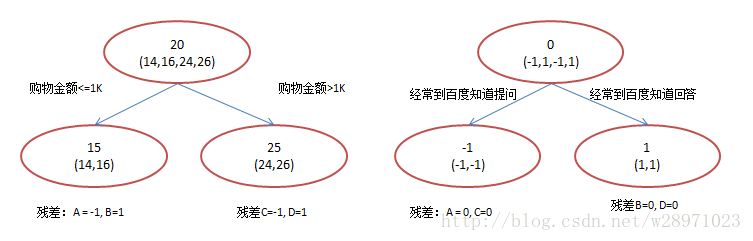
3.依据:
防止过拟合;
残差计算变相增大了分错样本的权重,分对的趋于0,这样后续的树就能专注于学习分错的样本;
每一步都用残差作为全局最优的梯度方向,并没有真实计算梯度;
每一次都走一小步,逐渐逼近目标,比每次都走一大步逼近目标更能防止过拟合。
4.优缺点:
优点:鲁棒性比较好,准确率比较高。
缺点:弱分类器间存在依赖关系,无法并行训练。
5.问题:
(1)训练过程:
gbdt通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练,通过降低偏差来不断提高最终分类器的精度。
(2)如何选择特征:
如CART,对每个节点的每个切分点进行遍历,选择基尼指数最小的。
(3)如何构建特征:
利用gbdt去产生特征的组合,以叶子结点为基,在基下的表示即为特征。
(4)如何用于分类:
针对样本 X 每个可能的类都训练一个分类回归树。
6.参考:
https://www.cnblogs.com/peizhe123/p/6105696.html
https://www.cnblogs.com/pinard/p/6140514.html
https://www.cnblogs.com/ModifyRong/p/7744987.html
三、Xgboost
1.思想:
Xgboost是GB算法的高效实现,xgboost中的基学习器除了可以是CART(gbtree)也可以是线性分类器(gblinear)
2.区别:
(1)xgboost在目标函数中显示的加上了正则化项,基学习为CART时,正则化项与树的叶子节点的数量T和叶子节点的值有关。
(2)GB中使用Loss Function对f(x)的一阶导数计算出伪残差用于学习生成fm(x),xgboost不仅使用到了一阶导数,还使用二阶导数。
(3)CART回归树中寻找最佳分割点的衡量标准是最小化均方差,xgboost寻找分割点的标准是最大化一个函数。
3.参考: