在学最短路是就看见了这个东西,觉得会很难,今天终于开学这个知识了
前向星是一个存图的工具,一种特殊的边集数组
所以前向星数组对应的其实是边的信息,下标就是边的下标
前向星
前向星
把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大
并且记录下以某个点为起点的所有边在数组中的起始位置和存储长度
len[i]数组记录以i为起点的边在数组中的储存长度
head[i]数组记录以i为边集在数组中的第一个存储位置(哪条边)
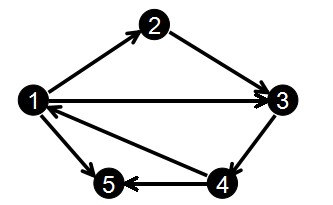
输入
1 2
2 3
3 4
1 3
4 1
1 5
4 5
排序得到的
编号 1 2 3 4 5 6 7
起点 1 1 1 2 3 4 4
终点 2 3 5 3 4 1 5
len[1]=3 head[1]=1
len[2]=1 head[2]=4
len[3]=1 head[3]=5
len[4]=2 head[4]=6
但是前向星会有排序操作,快排时间O(nlog(n))
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5;
int cnt = 0;
int head[N];//存储起点为Vi的第一条边的位置
struct note{
int from;
int to;
int w;
}edge[N];
bool cmp(note a, note b){//排序逻辑
if(a.from == b.from && a.to == b.to)return a.w < b.w;
if(a.from == b.from)return a.to < b.to;
return a.from < b.from;
}
void add(int u, int v, int w){
edge[cnt].from = u;
edge[cnt].to = v;
edge[cnt++].w = w;
}
int main(){
int n, m;
scanf("%d%d", &n, &m);
for(int i = 0; i < m; i++){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
add(u, v, w);
}
sort(edge, edge + m, cmp);
memset(head, -1 ,sizeof(head));
head[edge[0].from] = 0;
for(int i = 1; i < m; i++){
if(edge[i].from != edge[i - 1].from)//确定起点为Vi的第一条边的位置
head[edge[i].from] = i;
}
int start;
scanf("%d", &start);//输出某个确定点的连接情况
for(int k = head[start]; edge[k].from == start && k < m; k++){
cout << edge[k].from << " " << edge[k].to << " "<< edge[k].w << endl;
}
return 0;
}
链式前向星
链式前向星
利用链式取储存图的情况
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 1e4 + 5;
int head[N];//链式地址
int cnt = 0;//边的下标
struct node{
int next;//表示与第cnt条边同起点的上一条边的储存位置
int to;
int w;
}e[N << 1]; // 一般对一条无向边建立两条有向边
void add(int u, int v, int w){
e[cnt].w = w;//第cnt条边的权值是w
e[cnt].to = v;//第cnt条边的终点是v
e[cnt].next = head[u];//head[i]表示以i起点的最后一条边的储存位置
head[u] = cnt++;//head[];
}
int main(){
int n, m;
scanf("%d%d", &n, &m);
memset(head, 0, sizeof(head));
while(m--){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
add(u, v, w); add(v, u, w);
}
int start;
scanf("%d", &start);
for(int i = head[start]; i; i = e[i].next){//输出某个指定结点的连接情况
cout << start << "->" << e[i].to << " " << e[i].w << endl;
}
return 0;
}