快速排序算法可能是应用最广泛的算法,它流行的原因是它实现简单、适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。快速排序算法引人注目的特点包括它是原地排序(只需要一个很小的辅助栈),且将长度为N的数组排序所需的时间和NlgN成正比。——算法(第四版) p182
快速排序算法是一种分治的排序算法,它将一个数组分为两个子数组(这两个子数组,左边的子数组所有值都小于右边的子数组),再将两部分进行独立的排序,最终整个数组有序。
所以,快速排序的核心可以看成是:切分、分治。
1、分为两个子数组的关键是切分,快速排序的切分位置取决于数组的内容,选定一个切分元素(一般为数组第一个元素),将它放到合适的位置,使它左边的元素都小于这个分割元素,它右边的元素都大于这个切分元素。
假设V是数组第一个元素,选定它为切分元素。

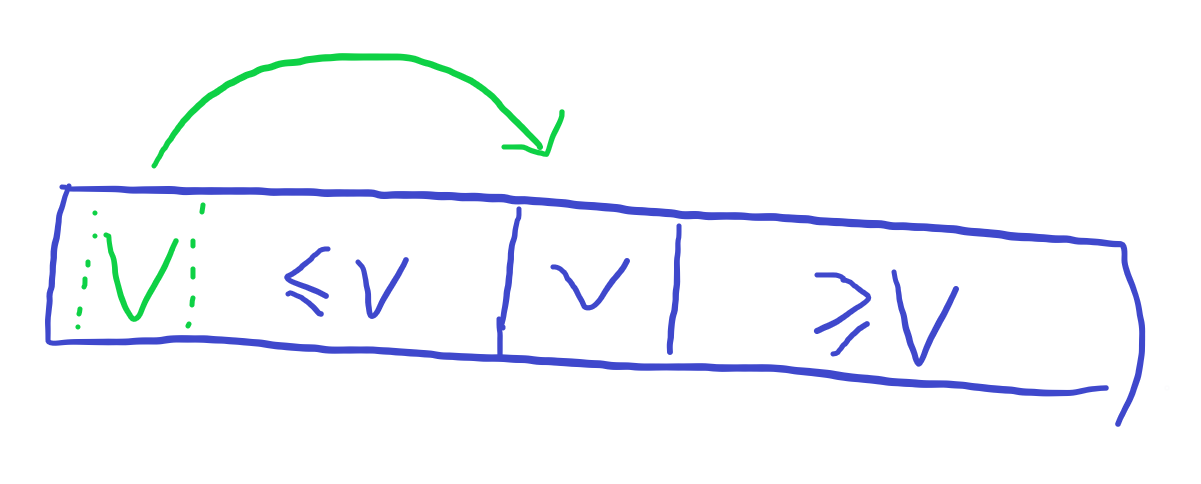
切分后数组应该是这样,V到数组中部的位置(不一定是中间),并且V左边的元素都小于V,V右边的元素都大于V。
假如我们继续对左边和右边进行切分,当最终只有一个元素时,整个数组会变得有序。
切分代码如下:
1 public static int partition(int[] arr,int left,int right){ 2 int i = left; //左扫描指针 3 int j = right; //右扫描指针 4 int temp = arr[i]; //切分元素 5 while (i < j) { //如果没扫描完(左右指针指向同一位置),就继续扫描 6 while( i<j && temp < arr[j]) //右指针向左扫描,如果右指针指向的元素比切分元素(temp)大,则继续向左扫描,如果遇到比切分元素小的,就停止。 7 j--; 8 if( i < j ){ //上一步停止扫描以后,有两种情况,i和j相遇,或者j指向的元素比i小,如果是第二种情况 就将j换到i的位置,然后i++ 开始i的扫描 9 arr[i++] = arr[j]; 10 } 11 12 while( i<j && temp > arr[i] ) //左指针向右扫描,原理同上 13 i++; 14 if (i < j) { 15 arr[j--] = arr[i]; 16 } 17 } 18 arr[i] = temp; //在扫描完成后 i和j指向同一位置,这个位置 左边的元素都小于右边的元素,这时将切分元素(temp)放在这个位置。 19 return i; //将切分元素所在下标返回,完成切分 20 }
此时,我们已经能正确切分数组了, 快速排序的主体应该是切分,然后再分别处理切分后的数组 , 所以代码可以这样:
1 public static void quickSort(int[] arr,int left,int right){ 2 if( left >= right) //递归调用的结束条件,当切分后的数组只有一个元素为止,此时左指针右指针相等 3 return; 4 int index = partition(arr,left,right); //获取切分的位置 5 quickSort(arr,left,index-1); //处理切分后左边的数组 left -> index-1 6 quickSort(arr,index+1,right); //处理切分后右边的数组 index+1 -> right 7 }
快速排序就完成了,如果将这两步合并在一起,就是这样:
1 public static void quickSort(int arr[],int left,int right){ 2 if (left < right) { //判断左右指针位置 3 int i = left; 4 int j = right; 5 int temp = arr[left]; 6 while(i<j){ 7 while(i<j && temp < arr[j]) 8 j--; 9 if( i < j ){ 10 arr[i++] = arr[j]; 11 } 12 while( i<j && temp > arr[i] ) 13 i++; 14 if (i < j) { 15 arr[j--] = arr[i]; 16 } 17 } 18 arr[i] = temp; 19 quickSort(arr,left,i-1); //分别处理另外两部分 20 quickSort(arr,i+1,right); 21 } 22 }
快速排序的平均时间复杂度是:O(nlogn)
附上各种排序算法的时间复杂度情况