INTERVIEW #4

120min, 5题。本菜鸡怒跪。

1、变身程序员

(读取时可以按行读取，直到读到空行为止，再对读取过的所有行做转换处理)
输出描述：
如果能将所有的产品经理变成程序员，输出最小的分钟数；
如果不能将所有的产品经理变成程序员，输出-1。
示例1：
输入：
0 2
1 0
输出：
-1
示例2：
输入：
1 2 1
1 1 0
0 1 1
输出：
3
示例3：
输入：
1 2
2 1
1 2
0 1
0 1
1 1
输出：
4

此题与https://leetcode.com/problems/rotting-oranges/类似。

基本思想就是将所有的程序员入队，BFS所有的产品经理，最后检查是否还有产品经理存在。

#define _CRT_SECURE_NO_WARNINGS

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include <queue>

using namespace std;

struct node {
    int x, y;
    int time;
    node() {}
    node(int xx, int yy, int t) :x(xx), y(yy), time(t) {}
};

queue<node> q;

int dir[4][2] = { {0,-1},{0,1},{-1,0},{1,0} };

int main()
{
    int grid[10][10];
    int row = 0, col = 0;
    string str;

    /*按行读取输入*/
    while (getline(cin, str))
    {
        col = 0;
        for (int i = 0; str[i]; i++)
        {
            if (str[i] != ' ')
            {
                grid[row][col++] = str[i] - '0';
            }
        }
        
        row++;
    }

    for(int i = 0;i < row;i++)
        for (int j = 0; j < col; j++)
        {
            if (grid[i][j] == 2)
            {
                //将所有程序员入队
                q.push(node(i, j, 0));
            }
        }

    node s;
    while (!q.empty())
    {
        s = q.front();

        /*四个方向遍历*/
        for (int i = 0; i < 4; i++)
        {
            int newx = s.x + dir[i][0];
            int newy = s.y + dir[i][1];

            //没有越界并且找到一枚产品经理
            if (newx >= 0 && newx < row && newy >= 0 && newy < col && grid[newx][newy] == 1)
            {
                grid[newx][newy] = 2;
                q.push(node(newx, newy, s.time + 1));
            }
        }
        q.pop();
    }

    for (int i = 0; i < row; i++)
        for (int j = 0; j < col; j++)
        {
            if (grid[i][j] == 1)
            {
                printf("-1
");
                return 0;
            }
        }

    printf("%d
", s.time);

    return 0;
}

2、特征提取

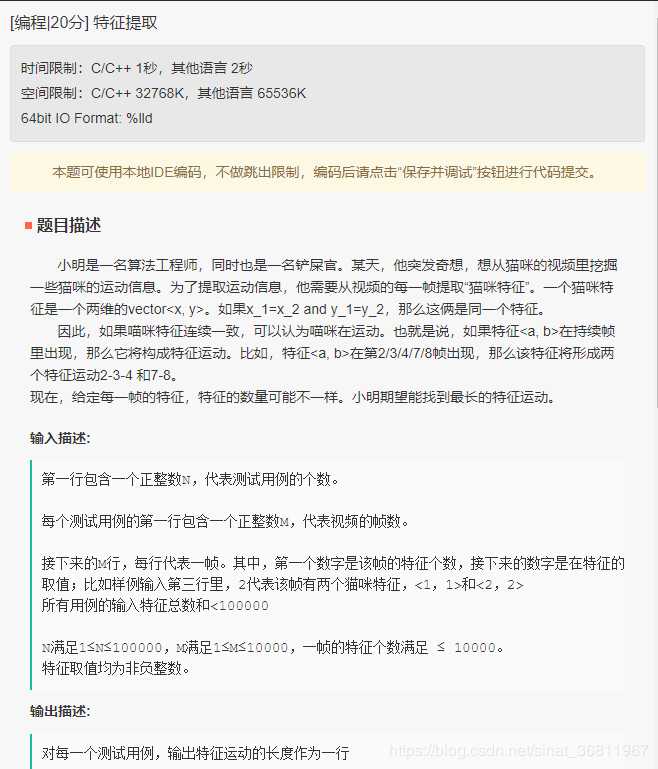
示例：
输入：
1
8
2 1 1 2 2
2 1 1 1 4 
2 1 1 2 2
2 2 2 1 4
0
0
1 1 1
1 1 1
输出：
3
说明：
特征<1，1>在连续的帧中出现3次，相比其他特征连续出现的次数大，所以输出3
备注：
如果没有长度大于2的特征运动，返回1

可以使用pair存储当前特征，使用map存储当前特征上一次出现的行数以及当前特征连续出现的长度。

还是对C++不熟唉

#define _CRT_SECURE_NO_WARNINGS

#include <cstdio>
#include <utility>
#include <map>
#include <algorithm>

using namespace std;

int main()
{
    int N, M, fea_num, res;
    scanf("%d", &N);

    while (N--)
    {
        scanf("%d", &M);
        res = 0;
        pair<int, int> cur;
        //当前特征上一次出现的行数以及连续出现的长度 
        map<pair<int, int>, int> lastIndex, length;
        for (int i = 0; i < M; i++)
        {
            scanf("%d", &fea_num);
            for (int j = 0; j < fea_num; j++)
            {
                scanf("%d%d", &cur.first, &cur.second);
                if (lastIndex[cur] == i)
                {
                    length[cur]++;
                }
                else
                {
                    length[cur] = 1;
                }
                lastIndex[cur] = i + 1;
                res = max(res, length[cur]);
            }
        }
        if (res <= 2)
            printf("1
");
        else
            printf("%d
", res);
    }

    return 0;
}

3、机器人跳跃

 

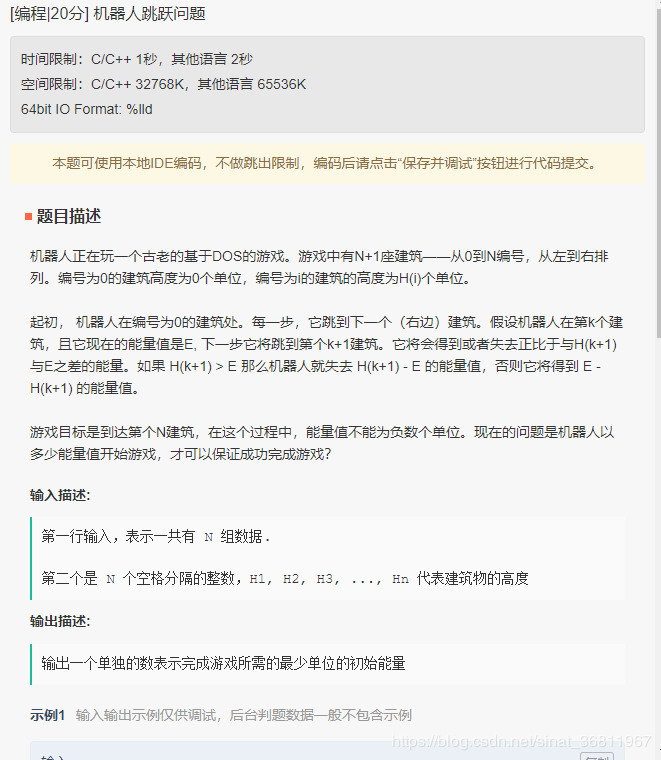
示例1：
输入：
5
3 4 3 2 4
输出：
4
示例2：
输入：
3
4 4 4
输出：
4
示例3：
输入：
3
1 6 4
输出：
3
备注：
1 <= N <= 10^5
1 <= H(i) <= 10^5

据说是小学数学，还想了半天。

根据题意可推出：$dp[k + 1] = 2*dp[k] - H[k + 1]$

#define _CRT_SECURE_NO_WARNINGS

#include <cstdio>
#include <cmath>
#include <vector>

using namespace std;

int main()
{
    int N;
    scanf("%d", &N);
    vector<int> H(N + 1);

    for (int i = 0; i < N; i++)
    {
        scanf("%d", &H[i + 1]);
    }

    vector<int> dp(N + 1);  //dp[k]表示从第k级开始需要的能量

    for (int i = N - 1; i >= 0; i--)
    {
        dp[i] = ceil((dp[i + 1] + H[i + 1]) / 2.0);
    }

    printf("%d
", dp[0]);

    return 0;
}

4、毕业旅行问题

 

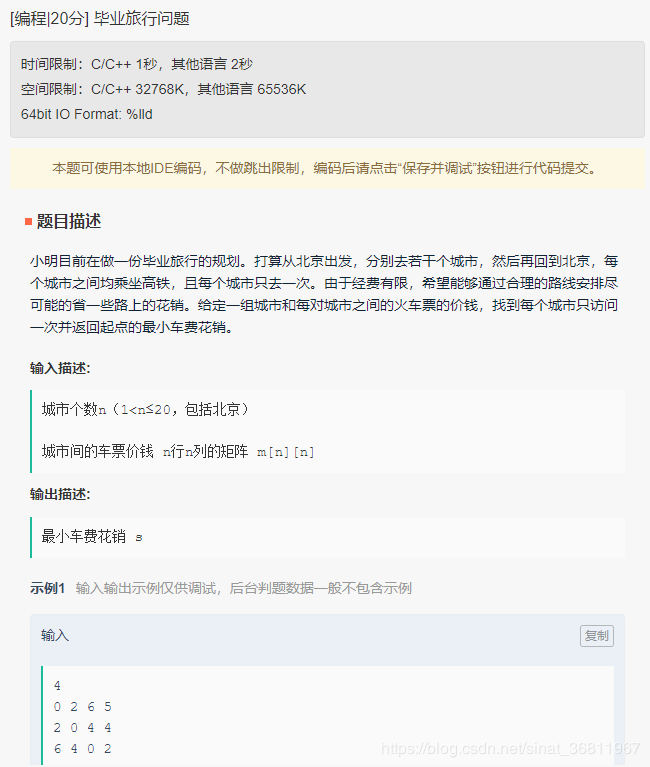
示例：
输入：
4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
输出：
13

典型的TSP问题，据说动态规划能够得到理论最优解，然而本渣看不懂状态转移方程。

贪心算法：从某城市出发，每次在未到达的城市中选择最近的一个，直到遍历完所有城市，最后回到出发地。

#define _CRT_SECURE_NO_WARNINGS

#include <cstdio>

using namespace std;

#define INF 1<<30;

int main()
{
    int n, m[20][20], res = 0;
    int edge_count = 0, flag[20] = { 1,0 };
    int cur = 0, next;
    scanf("%d", &n);

    for(int i = 0;i < n;i++)
        for (int j = 0; j < n; j++)
        {
            scanf("%d", &m[i][j]);
        }

    while (edge_count < n)
    {
        int min = INF;
        for (int j = 0; j < n; j++)
        {
            if (!flag[j] && m[cur][j] && m[cur][j] < min)
            {
                next = j;
                min = m[cur][j];
            }
        }
        res += m[cur][next];
        flag[next] = 1;
        edge_count++;
        cur = next;
    }

    res += m[cur][0];

    return 0;
}

5、过河

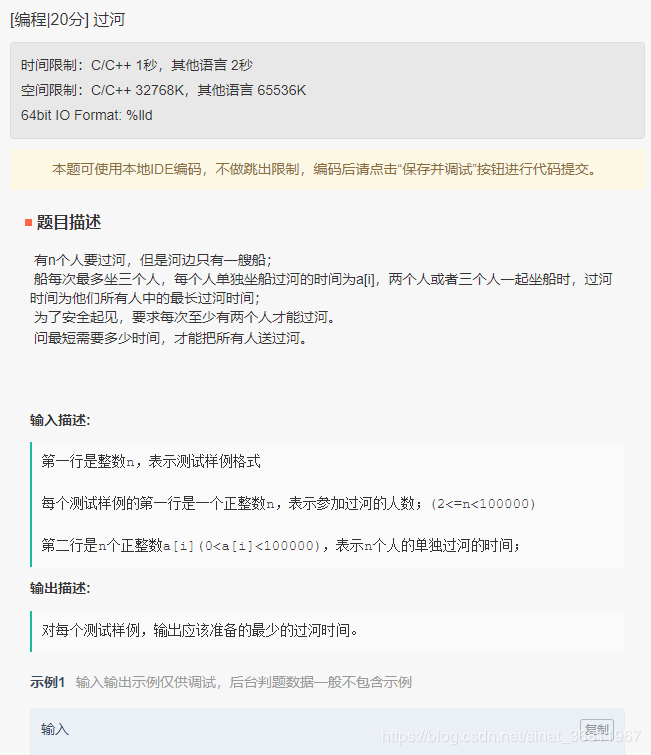
示例：
输入：
2
2
1 2
4
1 1 1 1
输出：
2
3

 每次过河只能2个或3个人，这种过河问题遵循“能者多劳”原则，即花费时间少的人折返去接其他人。

#define _CRT_SECURE_NO_WARNINGS

#include <cstdio>
#include <algorithm>

using namespace std;

int a[100010], dp[100010];

int main()
{
    int n, N;
    scanf("%d", &N);

    while (N--)
    {
        scanf("%d", &n);
        for (int i = 0; i < n; i++)
        {
            scanf("%d", &a[i]);
        }

        sort(a, a + n);
        dp[2] = a[1], dp[3] = a[2];
        for (int i = 4; i <= n; i++)
        {
            //前i个人过河的最短时间
            dp[i] = min( dp[i - 1] + a[0] + a[i - 1],dp[i - 2] + a[1] + a[i - 1] );
        }

        printf("%d
", dp[n]);
    }

    return 0;
}