J. Polygons Intersection
We will not waste your time, it is a straightforward problem. Given multiple polygons, calculate the area of their intersection. For simplicity, there will be exactly 2 polygons both of them are convex, given in the counterclockwise order and have non-zero areas. Furthermore, in one polygon a vertex won't be on the sides of the other one. The figure below demonstrates the first test case.
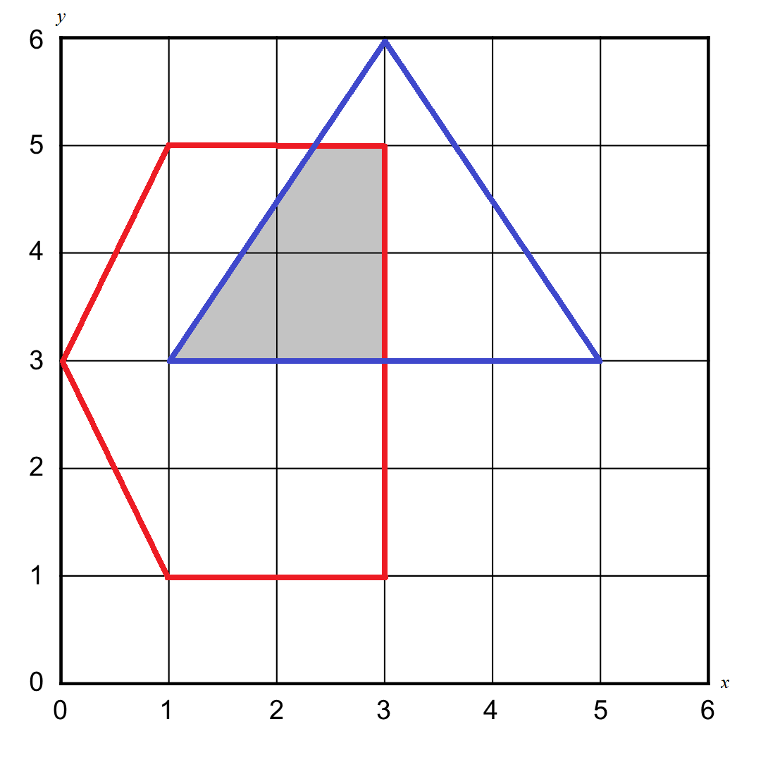
The first line of the input will be a single integer T, the number of test cases (1 ≤ T ≤ 20). each test case contains two integers (3 ≤ N, M ≤ 40) Then a line contains N pairs of integers xi, yi (-1000 ≤ xi, yi ≤ 1000) coordinates of the ith vertex of polygon A, followed by a line contains M pairs of integers xj, yj (-1000 ≤ xj, yj ≤ 1000) coordinates of the jth vertex of polygon B. The coordinates are separated by a single space.
For each test case, print on a single line, a single number representing the area of intersection, rounded to four decimal places.
2
5 3
0 3 1 1 3 1 3 5 1 5
1 3 5 3 3 6
3 3
-1 -1 -2 -1 -1 -2
1 1 2 1 1 2
2.6667
0.0000
题目链接:http://codeforces.com/gym/100952/problem/J
题意:给2个凸多边形,求相交面积
思路:板子题,学习一下!
下面给出AC代码:
1 #include "iostream" 2 #include "string.h" 3 #include "stack" 4 #include "queue" 5 #include "string" 6 #include "vector" 7 #include "set" 8 #include "map" 9 #include "algorithm" 10 #include "stdio.h" 11 #include "math.h" 12 #define ll long long 13 #define bug(x) cout<<x<<" "<<"UUUUU"<<endl; 14 #define mem(a) memset(a,0,sizeof(a)) 15 #define mp(x,y) make_pair(x,y) 16 using namespace std; 17 const long long INF = 1e18+1LL; 18 const int inf = 1e9+1e8; 19 const int N=1e5+100; 20 #define maxn 510 21 const double eps=1E-8; 22 int sig(double d){ 23 return(d>eps)-(d<-eps); 24 } 25 struct Point{ 26 double x,y; Point(){} 27 Point(double x,double y):x(x),y(y){} 28 bool operator==(const Point&p)const{ 29 return sig(x-p.x)==0&&sig(y-p.y)==0; 30 } 31 }; 32 double cross(Point o,Point a,Point b){ 33 return(a.x-o.x)*(b.y-o.y)-(b.x-o.x)*(a.y-o.y); 34 } 35 double area(Point* ps,int n){ 36 ps[n]=ps[0]; 37 double res=0; 38 for(int i=0;i<n;i++){ 39 res+=ps[i].x*ps[i+1].y-ps[i].y*ps[i+1].x; 40 } 41 return res/2.0; 42 } 43 int lineCross(Point a,Point b,Point c,Point d,Point&p){ 44 double s1,s2; 45 s1=cross(a,b,c); 46 s2=cross(a,b,d); 47 if(sig(s1)==0&&sig(s2)==0) return 2; 48 if(sig(s2-s1)==0) return 0; 49 p.x=(c.x*s2-d.x*s1)/(s2-s1); 50 p.y=(c.y*s2-d.y*s1)/(s2-s1); 51 return 1; 52 } 53 //多边形切割 54 //用直线ab切割多边形p,切割后的在向量(a,b)的左侧,并原地保存切割结果 55 //如果退化为一个点,也会返回去,此时n为1 56 void polygon_cut(Point*p,int&n,Point a,Point b){ 57 static Point pp[maxn]; 58 int m=0;p[n]=p[0]; 59 for(int i=0;i<n;i++){ 60 if(sig(cross(a,b,p[i]))>0) pp[m++]=p[i]; 61 if(sig(cross(a,b,p[i]))!=sig(cross(a,b,p[i+1]))) 62 lineCross(a,b,p[i],p[i+1],pp[m++]); 63 } 64 n=0; 65 for(int i=0;i<m;i++) 66 if(!i||!(pp[i]==pp[i-1])) 67 p[n++]=pp[i]; 68 while(n>1&&p[n-1]==p[0])n--; 69 } 70 //---------------华丽的分隔线-----------------// 71 //返回三角形oab和三角形ocd的有向交面积,o是原点// 72 double intersectArea(Point a,Point b,Point c,Point d){ 73 Point o(0,0); 74 int s1=sig(cross(o,a,b)); 75 int s2=sig(cross(o,c,d)); 76 if(s1==0||s2==0)return 0.0;//退化,面积为0 77 if(s1==-1) swap(a,b); 78 if(s2==-1) swap(c,d); 79 Point p[10]={o,a,b}; 80 int n=3; 81 polygon_cut(p,n,o,c); 82 polygon_cut(p,n,c,d); 83 polygon_cut(p,n,d,o); 84 double res=fabs(area(p,n)); 85 if(s1*s2==-1) res=-res;return res; 86 } 87 //求两多边形的交面积 88 double intersectArea(Point*ps1,int n1,Point*ps2,int n2){ 89 if(area(ps1,n1)<0) reverse(ps1,ps1+n1); 90 if(area(ps2,n2)<0) reverse(ps2,ps2+n2); 91 ps1[n1]=ps1[0]; 92 ps2[n2]=ps2[0]; 93 double res=0; 94 for(int i=0;i<n1;i++){ 95 for(int j=0;j<n2;j++){ 96 res+=intersectArea(ps1[i],ps1[i+1],ps2[j],ps2[j+1]); 97 } 98 } 99 return res;//assumeresispositive! 100 } 101 //hdu-3060求两个任意简单多边形的并面积 102 Point ps1[maxn],ps2[maxn]; 103 int n1,n2; 104 int main(){ 105 int t; 106 cin>>t; 107 while(t--){ 108 scanf("%d%d",&n1,&n2); 109 for(int i=0;i<n1;i++) 110 scanf("%lf%lf",&ps1[i].x,&ps1[i].y); 111 for(int i=0;i<n2;i++) 112 scanf("%lf%lf",&ps2[i].x,&ps2[i].y); 113 double ans=intersectArea(ps1,n1,ps2,n2); 114 //ans=fabs(area(ps1,n1))+fabs(area(ps2,n2))-ans;//容斥 115 printf("%.4f ",ans); 116 } 117 return 0; 118 }