Common Subsequence
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 39559 Accepted Submission(s): 18178
Problem Description
A
subsequence of a given sequence is the given sequence with some
elements (possible none) left out. Given a sequence X = <x1, x2, ...,
xm> another sequence Z = <z1, z2, ..., zk> is a subsequence of
X if there exists a strictly increasing sequence <i1, i2, ...,
ik> of indices of X such that for all j = 1,2,...,k, xij = zj. For
example, Z = <a, b, f, c> is a subsequence of X = <a, b, c, f,
b, c> with index sequence <1, 2, 4, 6>. Given two sequences X
and Y the problem is to find the length of the maximum-length common
subsequence of X and Y.
The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
The program input is from a text file. Each data set in the file contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct. For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
Sample Input
abcfbc abfcab
programming contest
abcd mnp
Sample Output
4
2
0
Source
Recommend
Ignatius
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1159
题目大意:给出两个字符串,求两个字符串的最长公共字串。
思路:这题是简单的动态规划题。以题目的第一组测试数据为例。(参考A_Eagle的题解)
abcfbc abfcab。
辅助空间变化示意图
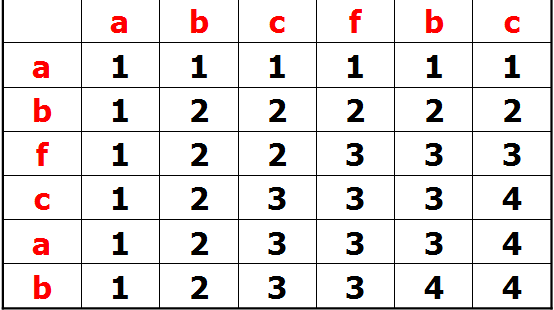
可以看出:
dp[i][j]=dp[i-1][j-1]+1;(a[i]==b[j])
dp[i][j]=max(dp[i-1][j],dp[i][j-1])(a[i]!=b[j]);
n由于F(i,j)只和dp(i-1,j-1), dp(i-1,j)和dp(i,j-1)有关, 而在计算dp(i,j)时, 只要选择一个合适的顺序, 就可以保证这三项都已经计算出来了, 这样就可以计算出dp(i,j). 这样一直推到dp(len(a),len(b))就得到所要求的解了.
下面给出AC代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 inline int read() 4 { 5 int x=0,f=1; 6 char ch=getchar(); 7 while(ch<'0'||ch>'9') 8 { 9 if(ch=='-') 10 f=-1; 11 ch=getchar(); 12 } 13 while(ch>='0'&&ch<='9') 14 { 15 x=x*10+ch-'0'; 16 ch=getchar(); 17 } 18 return x*f; 19 } 20 inline void write(int x) 21 { 22 if(x<0) 23 { 24 putchar('-'); 25 x=-x; 26 } 27 if(x>9) 28 { 29 write(x/10); 30 } 31 putchar(x%10+'0'); 32 } 33 char s1[1005],s2[1005]; 34 int dp[1005][1005]; 35 int main() 36 { 37 int len1,len2; 38 while(scanf("%s%s",s1+1,s2+1)!=EOF) 39 { 40 memset(dp,0,sizeof(dp)); 41 len1=strlen(s1+1),len2=strlen(s2+1); 42 for(int i=1;i<=len1;i++) 43 { 44 for(int j=1;j<=len2;j++) 45 { 46 if(s1[i]==s2[j] ) 47 dp[i][j]=dp[i-1][j-1]+1; 48 else 49 dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 50 } 51 } 52 printf("%d ",dp[len1][len2]); 53 } 54 return 0; 55 }