基数排序与桶排序，计数排序【详解】

桶排序简单入门篇^-^

在我们生活的这个世界中到处都是被排序过的东东。站队的时候会按照身高排序，考试的名次需要按照分数排序，网上购物的时候会按照价格排序，电子邮箱中的邮件按照时间排序……总之很多东东都需要排序，可以说排序是无处不在。现在我们举个具体的例子来介绍一下排序算法。

首先出场的是我们的主人公小哼，上面这个可爱的娃就是啦。期末考试完了老师要将同学们的分数按照从高到低排序。小哼的班上只有5个同学，这5个同学分别考了5分、3分、5分、2分和8分，哎，考得真是惨不忍睹（满分是10分）。接下来将分数进行从大到小排序，排序后是8 5 5 3 2。你有没有什么好方法编写一段程序，让计算机随机读入5个数然后将这5个数从大到小输出？请先想一想，至少想15分钟再往下看吧（*^__^*）。

我们这里只需借助一个一维数组就可以解决这个问题。请确定你真的仔细想过再往下看哦。

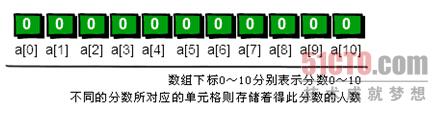
首先我们需要申请一个大小为11的数组int a[11]。OK，现在你已经有了11个变量，编号从a[0]~a[10]。刚开始的时候，我们将a[0]~a[10]都初始化为0，表示这些分数还都没有人得过。例如a[0]等于0就表示目前还没有人得过0分，同理a[1]等于0就表示目前还没有人得过1分……a[10]等于0就表示目前还没有人得过10分。

下面开始处理每一个人的分数，第一个人的分数是5分，我们就将相对应的a[5]的值在原来的基础增加1，即将a[5]的值从0改为1，表示5分出现过了一次。

第二个人的分数是3分，我们就把相对应的a[3]的值在原来的基础上增加1，即将a[3]的值从0改为1，表示3分出现过了一次。

注意啦！第三个人的分数也是5分，所以a[5]的值需要在此基础上再增加1，即将a[5]的值从1改为2，表示5分出现过了两次。

按照刚才的方法处理第四个和第五个人的分数。最终结果就是下面这个图啦。

你发现没有，a[0]~a[10]中的数值其实就是0分到10分每个分数出现的次数。接下来，我们只需要将出现过的分数打印出来就可以了，出现几次就打印几次，具体如下。

a[0]为0，表示“0”没有出现过，不打印。

a[1]为0，表示“1”没有出现过，不打印。

a[2]为1，表示“2”出现过1次，打印2。

a[3]为1，表示“3”出现过1次，打印3。

a[4]为0，表示“4”没有出现过，不打印。

a[5]为2，表示“5”出现过2次，打印5 5。

a[6]为0，表示“6”没有出现过，不打印。

a[7]为0，表示“7”没有出现过，不打印。

a[8]为1，表示“8”出现过1次，打印8。

a[9]为0，表示“9”没有出现过，不打印。

a[10]为0，表示“10”没有出现过，不打印。

最终屏幕输出“2 3 5 5 8”，完整的代码如下。

 1     #include <stdio.h> 
 2     int main()  
 3     {  
 4         int a[11],i,j,t;  
 5         for(i=0;i<=10;i++)  
 6             a[i]=0;  //初始化为0  
 7           
 8         for(i=1;i<=5;i++)  //循环读入5个数  
 9         {  
10             scanf("%d",&t);  //把每一个数读到变量t中  
11             a[t]++;  //进行计数  
12         }  
13      
14         for(i=0;i<=10;i++)  //依次判断a[0]~a[10]  
15             for(j=1;j<=a[i];j++)  //出现了几次就打印几次  
16                 printf("%d ",i);  
17      
18         getchar();getchar();   
19         //这里的getchar();用来暂停程序，以便查看程序输出的内容  
20         //也可以用system("pause");等来代替  
21         return 0;  
22     }

输入数据为：

5 3 5 2 8

仔细观察的同学会发现，刚才实现的是从小到大排序。但是我们要求是从大到小排序，这该怎么办呢？还是先自己想一想再往下看哦。

其实很简单。只需要将for(i=0;i<=10;i++)改为for(i=10;i>=0;i--)就OK啦，快去试一试吧。

这种排序方法我们暂且叫它“桶排序”。因为其实真正的桶排序要比这个复杂一些，以后再详细讨论，目前此算法已经能够满足我们的需求了。

这个算法就好比有11个桶，编号从0~10。每出现一个数，就在对应编号的桶中放一个小旗子，最后只要数数每个桶中有几个小旗子就OK了。例如2号桶中有1个小旗子，表示2出现了一次；3号桶中有1个小旗子，表示3出现了一次；5号桶中有2个小旗子，表示5出现了两次；8号桶中有1个小旗子，表示8出现了一次。

现在你可以尝试一下输入n个0~1000之间的整数，将它们从大到小排序。提醒一下，如果需要对数据范围在0~1000的整数进行排序，我们需要1001个桶，来表示0~1000之间每一个数出现的次数，这一点一定要注意。另外，此处的每一个桶的作用其实就是“标记”每个数出现的次数，因此我喜欢将之前的数组a换个更贴切的名字book（book这个单词有记录、标记的意思），代码实现如下。

 1     #include <stdio.h> 
 2      
 3     int main()  
 4     {  
 5         int book[1001],i,j,t,n;  
 6         for(i=0;i<=1000;i++)  
 7             book[i]=0;   
 8         scanf("%d",&n);//输入一个数n，表示接下来有n个数  
 9         for(i=1;i<=n;i++)//循环读入n个数，并进行桶排序  
10         {  
11             scanf("%d",&t);  //把每一个数读到变量t中  
12             book[t]++;  //进行计数，对编号为t的桶放一个小旗子  
13         }  
14         for(i=1000;i>=0;i--)  //依次判断编号1000~0的桶  
15             for(j=1;j<=book[i];j++)  //出现了几次就将桶的编号打印几次  
16                  printf("%d ",i);  
17      
18         getchar();getchar();  
19         return 0;  
20     }

可以输入以下数据进行验证。

8 100 50 22 15 6 1 1000 999 0

运行结果是：

1000 999 100 50 22 15 8 6 1 0

最后来说下时间复杂度的问题。代码中第6行的循环一共循环了m次（m为桶的个数），第9行的代码循环了n次（n为待排序数的个数），第14行和第15行一共循环了m+n次。所以整个排序算法一共执行了m+n+m+n次。我们用大写字母O来表示时间复杂度，因此该算法的时间复杂度是O(m+n+m+n)即O(2*(m+n))。我们在说时间复杂度的时候可以忽略较小的常数，最终桶排序的时间复杂度为O(m+n)。还有一点，在表示时间复杂度的时候，n和m通常用大写字母即O(M+N)。

这是一个非常快的排序算法。桶排序从1956年就开始被使用，该算法的基本思想是由E.J. Issac和R.C. Singleton提出来的。之前我说过，其实这并不是真正的桶排序算法，真正的桶排序算法要比这个更加复杂!

下面具体来说说基数排序和桶排序吧！

基数排序

基本思想

不进行关键字的比较,而是利用”分配”和”收集”。

PS：以十进制为例，基数指的是数的位，如个位，十位百位等。而以十六进制为例，0xB2，就有两个radices（radix的复数）。

Least significant digit（LSD）

短的关键字被认为是小的，排在前面，然后相同长度的关键字再按照词典顺序或者数字大小等进行排序。比如1，2，3，4，5，6，7，8，9，10，11或者”b, c, d, e, f, g, h, i, j, ba” 。

Most significance digit（MSD）

直接按照字典的顺序进行排序，对于字符串、单词或者是长度固定的整数排序比较合适。比如：1, 10, 2, 3, 4, 5, 6, 7, 8, 9和 “b, ba, c, d, e, f, g, h, i, j”。

基数排序图示

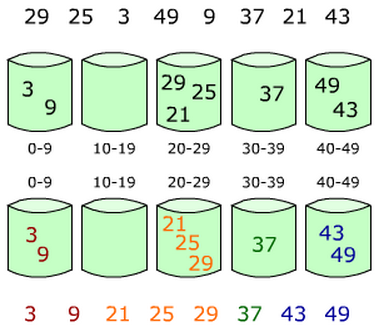
从图示中可以看出基数排序（LSD）的基本流程为如下节。

基数排序流程

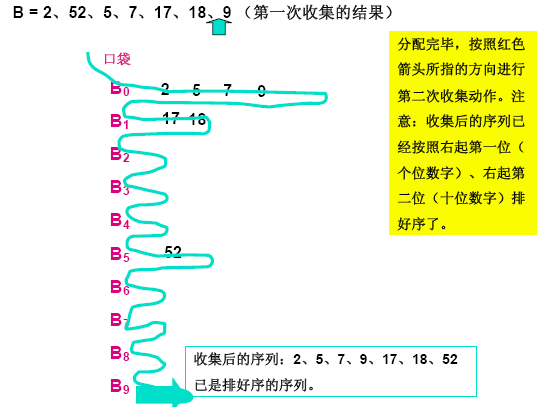
将根据整数的最右边数字将其扔进相应的0~9号的篮子里，对于相同的数字要保持其原来的相对顺序（确保排序算法的稳定性），然后将篮子里的数如图所示的串起来，然后再进行第二趟的收集（按照第二位的数字进行收集），就这样不断的反复，当没有更多的位时，串起来的数字就是排好序的数字。

算法分析

空间

采用顺序分配，显然不合适。由于每个口袋都有可能存放所有的待排序的整数。所以，额外空间的需求为10n，太

时间

上图示中每个数计有2 位，因此执行2 次分配和收集就可以了。在一般情况下，每个结点有d 位关键字，必须执行d 次分配和收集操作。

每次分配的代价：O(n)
每次收集的代价：O(radix)
总的代价为：O(d*(n+radix))

算法的c++ plus plus实现

基于LSD的基数排序算法：

 1 #include <iostream>
 2 
 3 using namespace std;
 4 const int MAX = 10;
 5 
 6 void print(int *a,int sz) {               
 7     for(int i = 0; i < sz; i++)
 8         cout << a[i] << " ";
 9     cout << endl;
10 }
11 
12 void RadixSortLSD(int *a, int arraySize)
13 {
14     int i, bucket[MAX], maxVal = 0, digitPosition =1 ;
15     for(i = 0; i < arraySize; i++) {
16         if(a[i] > maxVal) maxVal = a[i];
17     }
18 
19     int pass = 1;  // used to show the progress
20     /* maxVal: this variable decide the while-loop count 
21                if maxVal is 3 digits, then we loop through 3 times */
22     while(maxVal/digitPosition > 0) {
23         /* reset counter */
24         int digitCount[10] = {0};
25 
26         /* count pos-th digits (keys) */
27         for(i = 0; i < arraySize; i++)
28             digitCount[a[i]/digitPosition%10]++;
29 
30         /* accumulated count */
31         for(i = 1; i < 10; i++)
32             digitCount[i] += digitCount[i-1];
33 
34         /* To keep the order, start from back side */
35         for(i = arraySize - 1; i >= 0; i--)
36             bucket[--digitCount[a[i]/digitPosition%10]] = a[i];
37 
38         /* rearrange the original array using elements in the bucket */
39         for(i = 0; i < arraySize; i++)
40             a[i] = bucket[i];
41 
42         /* at this point, a array is sorted by digitPosition-th digit */
43         cout << "pass #" << pass++ << ": ";
44         print(a,arraySize);
45 
46         /* move up the digit position */
47         digitPosition *= 10;
48     }   
49  }
50 
51 int main()
52 {
53     int a[] = {170, 45, 75, 90, 2, 24, 802, 66};
54     const size_t sz = sizeof(a)/sizeof(a[0]);
55 
56     cout << "pass #0: ";
57     print(a,sz);
58     RadixSortLSD(&a[0],sz);
59     return 0;
60 }

输出为：

1 pass #0: 170 45 75 90 2 24 802 66 
2 pass #1: 170 90 2 802 24 45 75 66 
3 pass #2: 2 802 24 45 66 170 75 90 
4 pass #3: 2 24 45 66 75 90 170 802

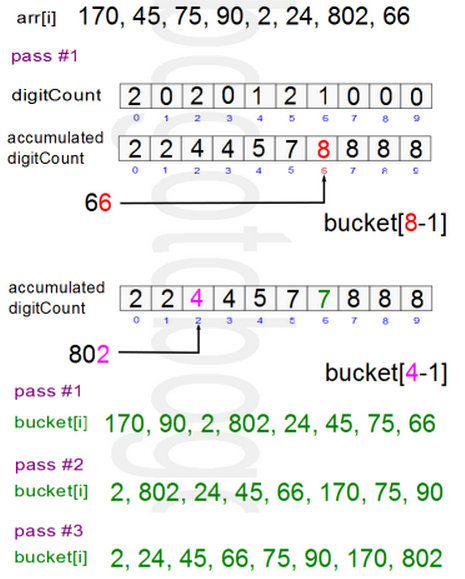
首先统计10个篮子（或口袋）中各有多少个数字，然后从0~9数字的频次分布（而不是频次密度，有一个累加的过程），以确定“收集”整数时的位置下标所在。同时为了保证排序算法稳定，相同的数字保持原来相对位置不变，对原始数据表倒序遍历，逐个构成收集后的数据表。例如，上图所示，对于数字66，其所对应的频次分布为8，也就是应当排在第8位，在数组中下标应该为7。而如果对于数字2和802，对应的频次分布为4，那么对于数据表从后往前遍历的话，对应802的下标为3，而2的下标2，这样实际上就保证了排序算法的稳定性。

桶排序（bucket sort）

基本思想

桶排序的基本思想是将一个数据表分割成许多buckets，然后每个bucket各自排序，或用不同的排序算法，或者递归的使用bucket sort算法。也是典型的divide-and-conquer分而治之的策略。它是一个分布式的排序，介于MSD基数排序和LSD基数排序之间。

基本流程

建立一堆buckets；
遍历原始数组，并将数据放入到各自的buckets当中；
对非空的buckets进行排序；
按照顺序遍历这些buckets并放回到原始数组中即可构成排序后的数组。

图示

算法的c++ plus plus描述

  1 #include <iostream>
  2 #include <iomanip>
  3 using namespace std;
  4 
  5 #define NARRAY 8  /* array size */
  6 #define NBUCKET 5 /* bucket size */
  7 #define INTERVAL 10 /* bucket range */
  8 
  9 struct Node 
 10 { 
 11     int data;  
 12     struct Node *next; 
 13 };
 14 
 15 void BucketSort(int arr[]);
 16 struct Node *InsertionSort(struct Node *list);
 17 void print(int arr[]);
 18 void printBuckets(struct Node *list);
 19 int getBucketIndex(int value);
 20 
 21 void BucketSort(int arr[])
 22 {   
 23     int i,j;
 24     struct Node **buckets;  
 25 
 26     /* allocate memory for array of pointers to the buckets */
 27     buckets = (struct Node **)malloc(sizeof(struct Node*) * NBUCKET); 
 28 
 29     /* initialize pointers to the buckets */
 30     for(i = 0; i < NBUCKET;++i) {  
 31         buckets[i] = NULL;
 32     }
 33 
 34     /* put items into the buckets */
 35     for(i = 0; i < NARRAY; ++i) {   
 36         struct Node *current;
 37         int pos = getBucketIndex(arr[i]);
 38         current = (struct Node *) malloc(sizeof(struct Node));
 39         current->data = arr[i]; 
 40         current->next = buckets[pos];  
 41         buckets[pos] = current;
 42     }
 43 
 44     /* check what's in each bucket */
 45     for(i = 0; i < NBUCKET; i++) {
 46         cout << "Bucket[" << i << "] : ";
 47             printBuckets(buckets[i]);
 48         cout << endl;
 49     }
 50 
 51     /* sorting bucket using Insertion Sort */
 52     for(i = 0; i < NBUCKET; ++i) {  
 53         buckets[i] = InsertionSort(buckets[i]); 
 54     }
 55 
 56     /* check what's in each bucket */
 57     cout << "-------------" << endl;
 58     cout << "Bucktets after sorted" << endl;
 59     for(i = 0; i < NBUCKET; i++) {
 60         cout << "Bucket[" << i << "] : ";
 61             printBuckets(buckets[i]);
 62         cout << endl;
 63     }
 64 
 65     /* put items back to original array */
 66     for(j =0, i = 0; i < NBUCKET; ++i) {    
 67         struct Node *node;
 68         node = buckets[i];
 69         while(node) {
 70             arr[j++] = node->data;
 71             node = node->next;
 72         }
 73     }
 74 
 75     /* free memory */
 76     for(i = 0; i < NBUCKET;++i) {   
 77         struct Node *node;
 78         node = buckets[i];
 79         while(node) {
 80             struct Node *tmp;
 81             tmp = node; 
 82             node = node->next; 
 83             free(tmp);
 84         }
 85     }
 86     free(buckets); 
 87     return;
 88 }
 89 
 90 /* Insertion Sort */
 91 struct Node *InsertionSort(struct Node *list)
 92 {   
 93     struct Node *k,*nodeList;
 94     /* need at least two items to sort */
 95     if(list == 0 || list->next == 0) { 
 96         return list; 
 97     }
 98 
 99     nodeList = list; 
100     k = list->next; 
101     nodeList->next = 0; /* 1st node is new list */
102     while(k != 0) { 
103         struct Node *ptr;
104         /* check if insert before first */
105         if(nodeList->data > k->data)  { 
106             struct Node *tmp;
107             tmp = k;  
108             k = k->next; 
109             tmp->next = nodeList;
110             nodeList = tmp; 
111             continue;
112         }
113 
114         for(ptr = nodeList; ptr->next != 0; ptr = ptr->next) {
115             if(ptr->next->data > k->data) break;
116         }
117 
118         if(ptr->next!=0){  
119             struct Node *tmp;
120             tmp = k;  
121             k = k->next; 
122             tmp->next = ptr->next;
123             ptr->next = tmp; 
124             continue;
125         }
126         else{
127             ptr->next = k;  
128             k = k->next;  
129             ptr->next->next = 0; 
130             continue;
131         }
132     }
133     return nodeList;
134 }
135 
136 int getBucketIndex(int value)
137 {
138     return value/INTERVAL;
139 }
140 
141 void print(int ar[])
142 {   
143     int i;
144     for(i = 0; i < NARRAY; ++i) { 
145         cout << setw(3) << ar[i]; 
146     }
147     cout << endl;
148 }
149 
150 void printBuckets(struct Node *list)
151 {
152     struct Node *cur = list;
153     while(cur) {
154         cout << setw(3) << cur->data;
155         cur = cur->next;
156     }
157 }
158 
159 int main(void)
160 {   
161     int array[NARRAY] = {29,25,3,49,9,37,21,43};
162 
163     cout << "Initial array" << endl;
164     print(array);
165     cout << "-------------" << endl;
166 
167     BucketSort(array); 
168     cout << "-------------" << endl;
169     cout << "Sorted array"  << endl;
170     print(array); 
171     return 0;
172 }

输出为：

 1 Initial array
 2  29 25  3 49  9 37 21 43
 3 -------------
 4 Bucket[0] :   9  3
 5 Bucket[1] :
 6 Bucket[2] :  21 25 29
 7 Bucket[3] :  37
 8 Bucket[4] :  43 49
 9 -------------
10 Bucktets after sorted
11 Bucket[0] :   3  9
12 Bucket[1] :
13 Bucket[2] :  21 25 29
14 Bucket[3] :  37
15 Bucket[4] :  43 49
16 -------------
17 Sorted array
18   3  9 21 25 29 37 43 49

虽然程序中的bucket采用链表结构以充分利用空间资源，而且bucket的构造也很巧妙，做的数据结构类似于栈链表的形式，插入都是插到顶部，所以后遍历的数据总是会在上面，因此从放入bucket之后的输出可以看出，跟图示进行对比，发现确实跟原来的原始相对顺序相反。

计数排序（counting sort）

目前介绍的利用比较元素进行排序的方法对数据表长度为 $n$

基本思想

当数据表长度为 $n$

基本操作

根据获得的数据表的范围，分割成不同的buckets，然后直接统计数据在buckets上的频次，然后顺序遍历buckets就可以得到已经排好序的数据表。

算法的c++ plus plus实现

 1 #include <iostream>
 2 
 3 using namespace std;
 4 
 5 void print(int a[], int sz) {
 6     for (int i = 0; i < sz;  i++ ) cout << a[i] << " ";
 7     cout << endl;
 8 }
 9 
10 void CountingSort(int arr[], int sz) {
11     int i, j, k;
12     int idx = 0;
13     int min, max;
14 
15     min = max = arr[0];
16     for(i = 1; i < sz; i++) {
17         min = (arr[i] < min) ? arr[i] : min;
18         max = (arr[i] > max) ? arr[i] : max;
19     }
20 
21     k = max - min + 1;
22     /* creates k buckets */
23     int *B = new int [k]; 
24     for(i = 0; i < k; i++) B[i] = 0;
25 
26     for(i = 0; i < sz; i++) B[arr[i] - min]++;
27     for(i = min; i <= max; i++) 
28         for(j = 0; j < B[i - min]; j++) arr[idx++] = i;
29 
30     print(arr,sz);
31 
32     delete [] B;
33 }
34 
35 int main()
36 {
37     int a[] = {5,9,3,9,10,9,2,4,13,10};
38     const size_t sz = sizeof(a)/sizeof(a[0]);
39     print(a,sz);
40     cout << "----------------------
" ;
41     CountingSort(a, sz);
42 }

输出为：

1 5 9 3 9 10 9 2 4 13 10
2 ----------------------
3 2 3 4 5 9 9 9 10 10 13

计算排序构造了k个buckets来统计数据频次，共需要两趟来实现排序，第一趟增量计数进行统计，第二趟将计数统计的对应的数重写入原始数据表中。

因为这种排序没有采用比较，所以突破了时间复杂度 $O (n l o g n)$

相关阅读:
c# 时间戳转换为Datetime类型的时间
 WCF小白初试错误之一：“有零个应用程序终结点”的解决办法
 对html制作新手的一些建议，大牛可以忽略
 Aspose.Words导出dt到word的问题
 获取checkboxlist选中的值以及绑定来自之前选中的来自数据库的值
 excel导入mssql数据库，支持excel2003--2010文件格式
 vscode调试angular
asp.net web api 跨域问题
 WPF 完美截图 <二>
EF错误
原文地址：https://www.cnblogs.com/ECJTUACM-873284962/p/6935506.html