Memory is now interested in the de-evolution of objects, specifically triangles. He starts with an equilateral triangle of side length x, and he wishes to perform operations to obtain an equilateral triangle of side length y.
In a single second, he can modify the length of a single side of the current triangle such that it remains a non-degenerate triangle (triangle of positive area). At any moment of time, the length of each side should be integer.
What is the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y?
The first and only line contains two integers x and y (3 ≤ y < x ≤ 100 000) — the starting and ending equilateral triangle side lengths respectively.
Print a single integer — the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y if he starts with the equilateral triangle of side length x.
6 3
4
8 5
3
22 4
6
In the first sample test, Memory starts with an equilateral triangle of side length 6 and wants one of side length 3. Denote a triangle with sides a, b, and c as (a, b, c). Then, Memory can do 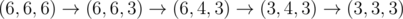 .
.
In the second sample test, Memory can do 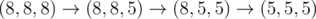 .
.
In the third sample test, Memory can do: 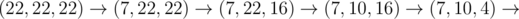
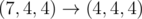 .
.
解题思路:
【题意】
现有边长为x的等边三角形,Memory想要将其变成边长为y的等边三角形
现规定Memory每秒能够改变一条边的大小,但要保证改变后的三条边仍能构成一个三角形
问,最少需要多少时间才能变为边长为y的等边三角形
【类型】
贪心,逆推
【分析】
从边长为6的等边三角形变为边长为3的等边三角形。先将一边变为3,则(6,6,3),如果再将一边变成3,则(6,3,3)并不能组成三角形,所以只能先变为(6,4,3)然后变为(3,4,3),最后变为(3,3,3),一共4步,所以输出4,此题很明显是贪心,直接贪就是了,用一个数记录需要的时间即可!此题需要注意的是最好选择逆推法,由y->x,这样就能保证合法且最快了!
【时间复杂度&&优化】
O(n)
题目链接→Codeforces Problem 712C Memory and De-Evolution
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int s[3]; 6 int x,y,i; 7 while(cin>>x>>y) 8 { 9 int ans=0; 10 s[0]=s[1]=s[2]=y; 11 for(i=0;s[0]<x||s[1]<x||s[2]<x;i++) 12 { 13 s[0]=s[1]+s[2]-1; 14 sort(s,s+3); 15 ans++; 16 } 17 cout<<ans<<endl; 18 } 19 return 0; 20 }
经过学长的提醒,我想出了另外一种方法,这样更简单!
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int s[3]; 6 int x,y,i; 7 while(cin>>x>>y) 8 { 9 s[0]=s[1]=s[2]=y; 10 for(i=0;s[0]<x||s[1]<x||s[2]<x;i++) 11 s[i%3]=s[(i+1)%3]+s[(i+2)%3]-1;//从小变大,每次都是最小边变另外两边的和减1,s[0],s[1],s[2]依次变就能保证,变时候一定是三个里面最小的 12 cout<<i<<endl; 13 } 14 return 0; 15 }
这样写也可以!
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 int s[3]; 6 int x,y,i; 7 while(cin>>x>>y) 8 { 9 s[0]=s[1]=s[2]=y; 10 int ans=0; 11 while(s[0]!=x||s[1]!=x||s[2]!=x) 12 { 13 sort(s,s+3); 14 s[0]=min(s[1]+s[2]-1,x); 15 ans++; 16 } 17 cout<<ans<<endl; 18 } 19 return 0; 20 }