原题链接在这里:https://leetcode.com/problems/all-paths-from-source-lead-to-destination/
题目:
Given the edges of a directed graph, and two nodes source and destination of this graph, determine whether or not all paths starting from source eventually end at destination, that is:
- At least one path exists from the
sourcenode to thedestinationnode - If a path exists from the
sourcenode to a node with no outgoing edges, then that node is equal todestination. - The number of possible paths from
sourcetodestinationis a finite number.
Return true if and only if all roads from source lead to destination.
Example 1:
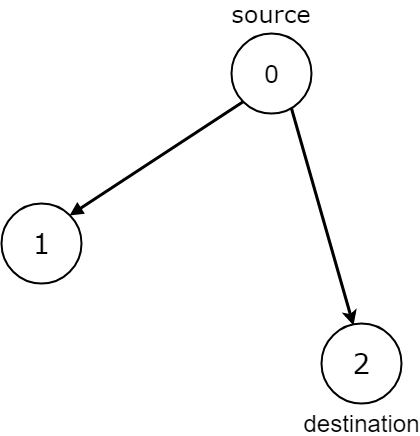
Input: n = 3, edges = [[0,1],[0,2]], source = 0, destination = 2
Output: false
Explanation: It is possible to reach and get stuck on both node 1 and node 2.
Example 2:
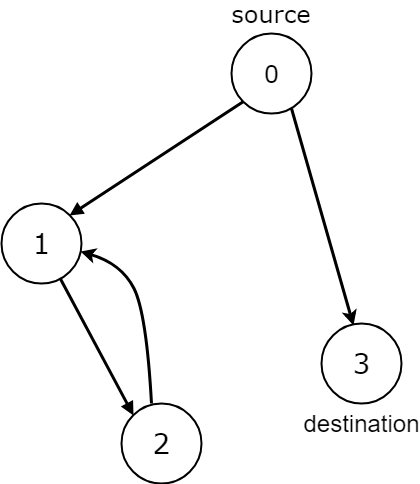
Input: n = 4, edges = [[0,1],[0,3],[1,2],[2,1]], source = 0, destination = 3
Output: false
Explanation: We have two possibilities: to end at node 3, or to loop over node 1 and node 2 indefinitely.
Example 3:
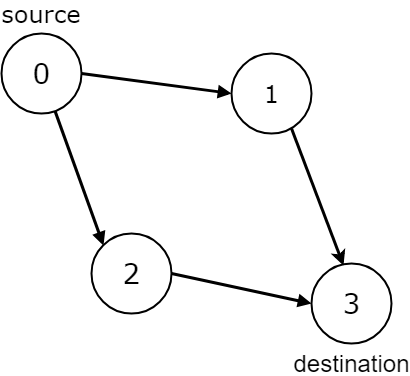
Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]], source = 0, destination = 3
Output: true
Example 4:
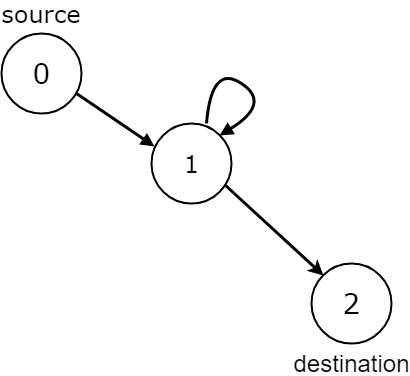
Input: n = 3, edges = [[0,1],[1,1],[1,2]], source = 0, destination = 2
Output: false
Explanation: All paths from the source node end at the destination node, but there are an infinite number of paths, such as 0-1-2, 0-1-1-2, 0-1-1-1-2, 0-1-1-1-1-2, and so on.
Example 5:
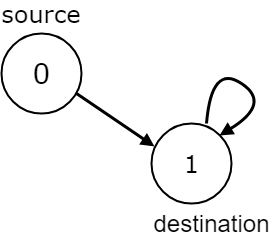
Input: n = 2, edges = [[0,1],[1,1]], source = 0, destination = 1
Output: false
Explanation: There is infinite self-loop at destination node.
Note:
- The given graph may have self loops and parallel edges.
- The number of nodes
nin the graph is between1and10000 - The number of edges in the graph is between
0and10000 0 <= edges.length <= 10000edges[i].length == 20 <= source <= n - 10 <= destination <= n - 1
题解:
There are 2 cases it should return false.
case 1: it encounters a node that has no outgoing edges, but it is not destination.
case 2: it has cycle.
Otherwise, it returns true.
Could iterate graph with BFS. When indegree of a node becomes negative, then ther is cycle.
Time Complexity: O(n+e). e = edges.length.
Space: O(n+e).
AC Java:
1 class Solution { 2 public boolean leadsToDestination(int n, int[][] edges, int source, int destination) { 3 Set<Integer> [] graph = new Set[n]; 4 5 for(int i = 0; i<n; i++){ 6 graph[i] = new HashSet<Integer>(); 7 } 8 9 int [] inDegrees = new int[n]; 10 for(int [] edge : edges){ 11 graph[edge[0]].add(edge[1]); 12 inDegrees[edge[1]]++; 13 } 14 15 LinkedList<Integer> que = new LinkedList<Integer>(); 16 que.add(source); 17 18 while(!que.isEmpty()){ 19 int cur = que.poll(); 20 if(graph[cur].size() == 0 && cur != destination){ 21 return false; 22 } 23 24 for(int nei : graph[cur]){ 25 if(inDegrees[nei] < 0){ 26 return false; 27 } 28 29 inDegrees[nei]--; 30 31 que.add(nei); 32 } 33 } 34 35 return true; 36 } 37 }
Could iterate by DFS too.
If current node has been visited within current DFS, then there is cycle.
When traversing all the nodes, make current node as done.
Time Complexity: O(n+e).
Space: O(n+e).
AC Java:
1 class Solution { 2 public boolean leadsToDestination(int n, int[][] edges, int source, int destination) { 3 Set<Integer> [] graph = new Set[n]; 4 for(int i = 0; i<n; i++){ 5 graph[i] = new HashSet<Integer>(); 6 } 7 8 for(int [] edge : edges){ 9 graph[edge[0]].add(edge[1]); 10 } 11 12 return dfs(source, destination, graph, new int[n]); 13 } 14 15 private boolean dfs(int cur, int destination, Set<Integer> [] graph, int [] visited){ 16 if(visited[cur] != 0){ 17 return visited[cur] == 2; 18 } 19 20 if(graph[cur].size() == 0){ 21 return cur == destination; 22 } 23 24 visited[cur] = 1; 25 for(int nei : graph[cur]){ 26 if(!dfs(nei, destination, graph, visited)){ 27 return false; 28 } 29 } 30 31 visited[cur] = 2; 32 return true; 33 } 34 }