
【题解】
1,本题要求维护一个序列,支持区间加k,询问区间平均数和方差。
2,询问平均数显然很好处理,在线段树上维护区间和sum以及区间长度len即可。
3,方差的处理就相对麻烦一些。需要研究一下公式。
我们先看看方差的公式:

那就是1/n乘上这个式子: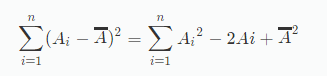
也就是区间平方和Sqr-区间和Sum的两倍+平均数Ave的平方乘区间长Len,所得结果再除以区间长Len
那么我们在线段树上再维护一个区间平方和Sqr就好了
4,在区间修改的时候,怎么维护Sqr呢?我们可以发现修改后的平方和为:
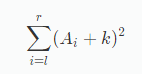 (k是区间加上的数)
(k是区间加上的数)
展开式子就是:
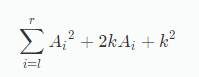
那就是原来的Sqr+原来的Sum乘k乘2+k的平方乘区间长Len
这样,我们就可以解决这个问题了
#include<cstdio>
#include<algorithm>
#define N (800010)
#define ls (u<<1)
#define rs (u<<1|1)
#define mid ((a[u].l+a[u].r)>>1)
#define len(x) (a[x].r-a[x].l+1)
using namespace std;
int n,m,opt,x,y;
double del,sqr,sum;
struct tree{
int l,r;
double del,sum,sqr;
}a[N];
inline int read(){
int k=0,f=1; char c=getchar();
while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar();
while('0'<=c&&c<='9')k=k*10+c-'0',c=getchar();
return k*f;
}
inline void pushup(int u){
a[u].sum=a[ls].sum+a[rs].sum;
a[u].sqr=a[ls].sqr+a[rs].sqr;
}
inline void pushdown(int u){
if(!a[u].del) return; double D=a[u].del; a[u].del=0;
a[ls].del+=D; a[ls].sqr+=a[ls].sum*D*2+D*D*len(ls); a[ls].sum+=len(ls)*D;
a[rs].del+=D; a[rs].sqr+=a[rs].sum*D*2+D*D*len(rs); a[rs].sum+=len(rs)*D;
}
void build(int u,int l,int r){
a[u].l=l; a[u].r=r;
if(l<r) build(ls,l,mid),build(rs,mid+1,r),pushup(u);
else scanf("%lf",&a[u].sum),a[u].sqr=a[u].sum*a[u].sum;
}
void update(int u,int l,int r,double del){
if(l<=a[u].l&&a[u].r<=r){
a[u].sqr+=a[u].sum*del*2+del*del*len(u);
a[u].sum+=len(u)*del;
a[u].del+=del;
return;
}
pushdown(u);
if(l<=mid) update(ls,l,r,del);
if(r>mid) update(rs,l,r,del);
pushup(u);
}
void query(int u,int l,int r,double &sqr,double &sum){
if(l<=a[u].l&&a[u].r<=r){
sqr+=a[u].sqr; sum+=a[u].sum;
return;
}
pushdown(u);
if(l<=mid) query(ls,l,r,sqr,sum);
if(r>mid) query(rs,l,r,sqr,sum);
}
int main(){
n=read(); m=read();
build(1,1,n);
while(m--){
if((opt=read())==1) x=read(),y=read(),scanf("%lf",&del),update(1,x,y,del);
if(opt==2){
sum=0; sqr=0;
x=read(); y=read();
query(1,x,y,sqr,sum);
printf("%.4lf
",1.0*sum/(y-x+1));
}
if(opt==3){
sum=0; sqr=0;
x=read(); y=read(); int l=y-x+1;
query(1,x,y,sqr,sum);
double ave=1.0*sum/l;
//printf("sqr=%.4f sum=%.4f
",sqr,sum);
printf("%.4lf
",(sqr-2*sum*ave+l*ave*ave)/l);
}
}
return 0;
}