凸优化
作者：樱花猪
摘要:
本文为七月算法（julyedu.com）12月机器学习第四次课在线笔记。“凸优化”指的是一种比较特殊的优化，通过“凸优化”我们能够把目标函数转化成一个“凸函数”然后利用凸函数的性质求极值来求解问题。“凸优化”不仅仅在机器学习中有所应用，几乎在任何用到有关于目标函数求值的问题都会用到。本次课程由浅入深，将学术上复杂的问题解释的通俗易懂，个人认为是机器学习系列课程非常有亮点的一课。
引言：
本文用凸函数结合凸集的视角来阐述凸优化的方案，在课程中提供了一些简单易操作的例子让看起来比较阳春白雪的凸优化问题变得非常接地气。这次课程的内容不仅仅可以运用到机器学习，还可以用于许多将优化目标函数的问题中。本次比较比较注重于基础概念的记录以及算法的思路而不过多纠结定理的证明。
预备知识：
高等数学
预备概念：
凸集保凸运算；分割超平面；支撑超平面；上境图；Jensen不等式；凸函数的保凸运算；
凸优化：
KKT条件；
一、预备知识
1、直线的向量表达：
假设直线经过两点A、B，则：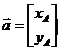
，
,
；
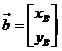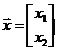当
时，
表示过AB的直线。
当
时，
表示过AB的线段。
2、几何体的向量表达
任何体都可以用向量表达
三维平面：
超平面：
（超）几何体：
3、仿射集
定义：通过集合C中任意两个不同点的直线仍然在集合C内，则称集合C为仿射集。
类比几何体向量表达中的平面表达，多点的时候要满足
4、凸集
集合C内任意两点间的线段均在集合C内， 则称集合C为凸集。
类比几何体向量表达中的几何体表达，多点的时候要满足
因为仿射集的条件比凸集的条件强，所以，仿射集必然是凸集。
5、凸包
集合C的所有点的凸组合形成的集合，叫做集C的凸包。
集合C的凸包是能够包含C的最小的凸集。
6、超平面和半空间
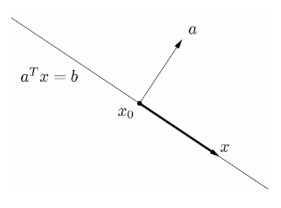
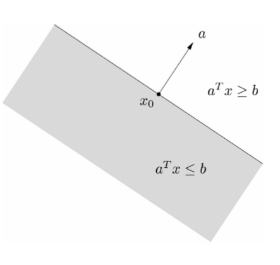
半空间half space
7、欧式球和椭球
欧式球：
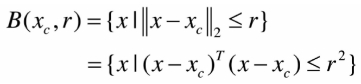
椭球：
。
8、范数：
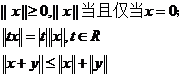
9、范数球
10、范数锥
11、多面体
多面体有限个半空间和超平面的交集。
仿射集(如超平面、直线)、射线、线段、半空间都 是多面体。
多面体是凸集。
12、保凸运算
集合交运算：仿射变换（线性变换
）
透视变换：透视函数对向量进行伸缩(规范化)，使得最 后一维的分量为1并舍弃之。（降维）
投射变换：投射函数是透视函数和仿射函数的复合
13、支撑超平面
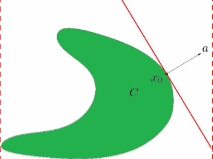
14、凸函数
15、上境图
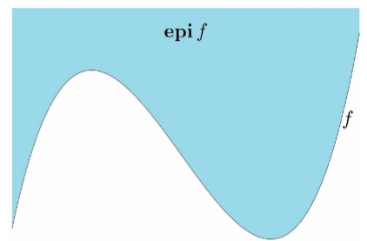
16、凸函数与凸集
一个函数是凸函数，当且仅当其上境图是凸集，（凸优化重要思路）
17、Jesen不等式
若f是凸函数：
18、保持函数凸性的算子
a. 凸函数的非负加权和
b. 凸函数与仿射函数的复合
c. 凸函数的逐点最大值、逐点上确界
19、共轭函数
原函数
共轭函数定义：
定义式的右端是关于y的仿射函数，它们逐点求上确界，得到的函数f*(y)一定是凸函数。
20、Fenchel不等式
根据共轭函数定义有：
二、凸优化
凸优化的基本形式：
目标：求f(x)的最小值解。
条件：
凸函数：
；
仿射函数：
凸优化问题的重要性质：
凸优化问题的可行域为凸集
凸优化问题的局部最优解即为全局最优解（非常重要）
根据凸优化问题的基本形式，很容易想到拉格朗日乘子法。
构造拉格朗日函数：
对固定的x，Lagrange函数L(x,λ,v)为关于λ和v的仿射函数
求下界，即Lagrange对偶函数
若原优化问题有最值
，则
于是我们希望Lagrange对偶函数为凹函数。
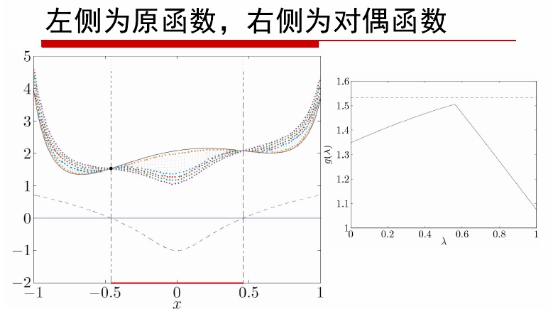
于是我们希望求右图的上界。
若要对偶函数的最大值即为原问题的最小值，考察需要满足的条件：
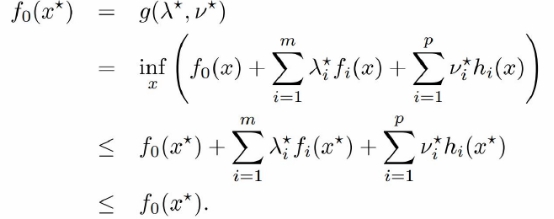
最后得到KKT条件：
