（二叉）堆

 

基本概念

堆（也叫优先队列），特点是父节点的值大于（小于）两个子节点的值（分别称为大顶堆和小顶堆）。

 

介绍

In a heap, the highest (or lowest) priority element is always stored at the root. A heap is not a sorted structure and can be regarded as partially ordered. As visible from the heap-diagram, there is no particular relationship among nodes on any given level, even among the siblings. When a binary heap is a complete binary tree, it has a smallest possible height for a binary heap—a heap with N nodes always has log N height. A heap is a useful data structure when you need to remove the object with the highest (or lowest) priority.（wiki）

 

---

逻辑与存储结构

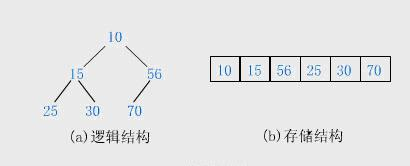
堆的逻辑结构是一棵完全二叉树，高度为O（lg n），其基本操作至多与树的高度成正比（即 <= n O（lg n））；物理结构一般用数组来存储。完全二叉树特点：

1. n个结点，则深度为 [ log2（n）] + 1
2. 完全二叉树下标关系：

• （顺序表存储，下标从1开始）：双亲[ i / 2 ] 、左孩子 2 * i 、右孩子 2 * i + 1 
• （顺序表存储，下标从0开始）： 亲 [ （i-1） / 2 ] 、左孩子 2 * i + 1、右孩子 2 * i + 2

 

建立/调整堆：O（lg n）

堆排序：n O（lg n）

 

---

基本操作

（数组下标从1开始）

找最大最小值

堆顶即是

 

调整堆结构

1.    //（子堆已经建好后）调整堆顶
2. //从小到大排：建立最大堆
3.     publicvoid sift(int[] r,int k,int m //k：堆顶序号  m：最后节点序号
4. {       
5.         int i = k , j =2* i;                  //i：堆顶序号  j：堆顶孩子节点序号
6.  
7.         while(j <= m){
8.             if(j < m && r[j]< r[j+1]) j++;     //j为左右子节点中较大的
9.  
10.             if(r[i]< r[j]){                    //交换父子节点
11.                 int temp = r[i];
12.                 r[i]= r[j];
13.                 r[j]= temp;
14.  
15.                 i = j;  j =2* i;              //调整改变堆顶后的子堆
16.             }
17.             elsebreak;
18.         }
19.  
20.     }

 

建堆

 

1. //由下至上建立堆

2. for (int i = n/2; i >=1; i--)
3.         sift(r,i,n);

 

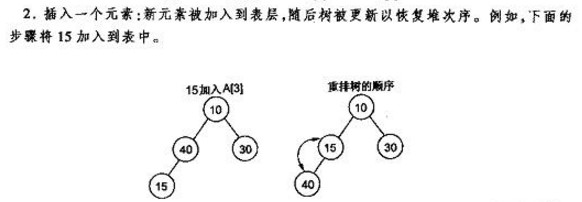
插入

在数组的尾部插入元素，然后重新自下往上建堆

 

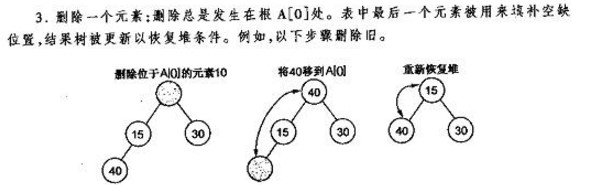
删除

删除堆顶，把数组最后一个元素交换上来，对堆顶重新调整堆结构

 

替代

替代堆顶，对堆顶重新调整堆结构

 

---

堆的应用

 

• 优先队列

    The Java platform (since version 1.5) provides the binary heap implementation with class java.util.PriorityQueue<E> in Java Collections Framework. This class implements by default a min-heap; to implement a max-heap, programmer should write a custom comparator. There is no support for the decrease/increase-key operation.

 

• 堆排序

    时间复杂度为O(N lg N)。如果是从小到大排序，用大顶堆；从大到小排序，用小顶堆。

 

• 一个文件中包含了1亿个随机整数，如何快速的找到最大(小)的100万个数字?（时间复杂度：O（n lg k））（海量数据前n大，并且n比较小，则堆可以放入内存）

    取前100 万个整数，建立小顶堆，然后接着依次取下一个整数，如果它大于最小元素亦即堆顶元素，则将其赋予堆顶元素（替代），然后对堆顶重新调整整个堆。然后继续取下一个整数，如此下去，则最后留在堆中的100万个整数即为所求 100万个数字。该方法可大大节约内存。

 

• 找出第k个最大值

    维护一个k大小的最小堆，对于数组中的每一个元素判断与堆顶的大小，若堆顶较大，则不管，否则，弹出堆顶，将当前值插入到堆中。时间复杂度O(n * logk)。

 

• 在O(n lg k)时间内，将k个n长（不一定等长）的有序表合并成一个有序表

    假设有k个有序容器，我们希望把这些容器里面的元素有序地放到一个大容器里面去。

    我们姑且称k个有序容器为小容器。对每个小容器维护一个cursor，cursor刚开始指向小容器中的第一个元素，即最小的元素。每个循环中，对k个cursor指向的元素建立一个最小堆；从这个堆里面extract最小的元素加到大容器里面；被extract最小元素的那个小容器的cursor往后挪一位；进入下一个循环。如果一个容器的cursor到达end了，那么最小堆的大小减一。

    因为我们每次加入到大容器里面的都是当前所有小容器中最小的元素，所以大容器是有序的。 

 

• 一组不断产生的随机数中找到并维持中位数的值。（英文表述：numbers are randomly generated and passed to a method. Write a program to find and maintain the median value as new values are generated.）

    维持一个最大堆和一个最小堆。最大堆维持小于median的元素，最小堆维持大于median的元素。如果新进来的元素比median小，就插入最大堆；比median大，就插入最小堆。同时两个堆的size始终是相等或者相差一个：当这个性质由于按前面所述方法插入两个堆后而被破坏（失衡）时，只要把median放入少元素的一个堆，从多元素的堆取出堆顶作为median即可。

 

 

 

 

资料整理自网络（侵删）
整理by Doing