http://www.cnblogs.com/xing901022/p/9332529.html
本章主要讲解了逻辑回归相关的问题,比如什么是分类?逻辑回归如何定义损失函数?逻辑回归如何求最优解?如何理解决策边界?如何解决多分类的问题?
更多内容参考 机器学习&深度学习
有的时候我们遇到的问题并不是线性的问题,而是分类的问题。比如判断邮件是否是垃圾邮件,信用卡交易是否正常,肿瘤是良性还是恶性的。他们有一个共同点就是Y只有两个值{0,1},0代表正类,比如肿瘤是良性的;1代表负类,比如肿瘤是恶性的。当然你想用1代表良性也可以,而且输出的值不仅仅局限为0和1两类,有可能还有多类,比如手写体识别是从0到9。

如果使用线性的方法来判断分类问题,就会出现图上的问题。我们需要人工的判断中间的分界点,这个很不容易判断;如果在很远的地方有样本点,那么中心点就会发生漂移,影响准确性。

如果我们想要结果总是在0到1之间,那么就可以使用sigmoid函数,它能保证数据在0-1之间。并且越趋近于无穷大,数据越趋近于1。
回到我们假设的问题上来,如果肿瘤是依赖于大小来判断良性恶性,如果超过0.7*平均值,就判断是恶性的,那么平均来算30%的是恶性的,70%是良性的,他们相加总会是100%。再来看看上面的sigmoid的图像,每个点都表示它属于1的概率是x,属于0的概率是1-x。这样一个分类的问题,就变成了曲线值得问题了。
如果想让y=1,即g(z)的值要大于0.5,那么z的值就需要大于0;相反,y=0,就是z的值小于0。因此整个分类问题,就变成了寻找决策边界的问题了。
那么如何确定逻辑回归的损失函数呢?如果使用均方误差,由于最终的值都是0和1,就会产生震荡,此时是无法进行求导的。
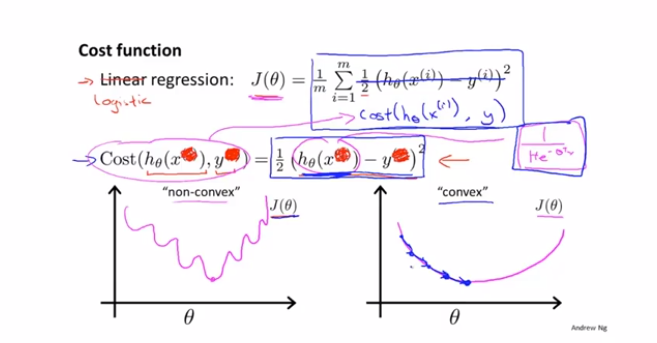
因此需要寻找一个方法,使得代价函数变成凸函数,从而易于求解。


如果把损失函数定义为上面的形式,当真实的值是1时,我们预测的值越靠近1,cost的值越小,误差越小。如果真实值是0,那么预测的值越靠近1,cost的值越大。完美的表达了损失的概念。而且,由于0和1的概念,可以把上面的公式合并成下面统一的写法。直接基于这个统一的写法,做梯度下降求解即可。

在求解最优化的问题时,不仅仅只有一种梯度下降Gradient descenet,还可以使用Conjugate gradient,BFGS,L-BFSGS。
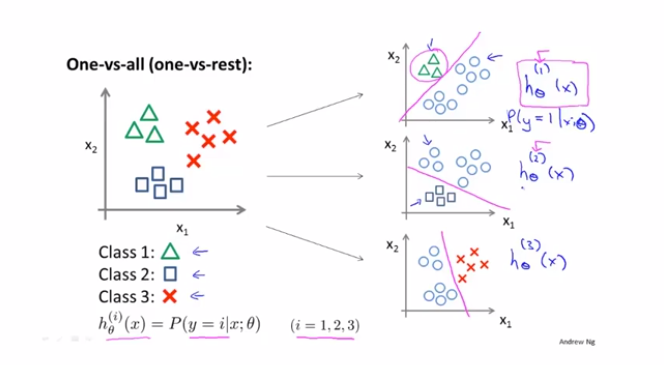
多分类问题,可以理解为采用多个logistic分类器,进行分类。针对每个样本点进行一个预测,给出概率值,选择概率值最高的那个进行分类的标识。