cf 1437F.Emotional Fishermen（计数dp）

题目链接：传送门

题目思路：

题目思路参考于博客：&*^*&(

题目是关于前缀最大值的，那么不妨先将a数组排序，定义dp(i,j) 表示长度为 i 且最大元素为 a_j 的合法排列个数；

根据排序后的单调性，预处理出 pos_i ，pos_i 的值是满足 a_j * 2 <= a_i 的最大的 j ； 

所谓合法，即满足下式：（p数组是1-n的排列）

　　

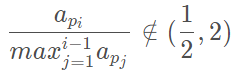
现在考虑dp(i,j)的转移：

　　首先排列的最大值为a_j ，那么其他 i -1 个项是一定 <= a_j / 2 的，且保证合法，

　　1）dp(i,j) <- dp(i-1,j) * max( 0 , pos_j - i + 2 ) ；

　　　如果是前 i-1 项 的最大元素已经是 a_j 了，那么第 i 个位置 能填写的数字个数为 pos_j - i +2 个（前面有一个a_j 和 i-2 个 a_k ，k<=pos_j ，这个位置就只剩下 pos_j - (i-2) 个数字可填 ）；

　　2）dp(i,j) <- Σdp(i-1,k) ,  k≥1 && k≤pos_j ；（前缀和优化）

　　　如果前 i-1 项的最大元素不为a_j ，由第 i 个位置 加入 a_j 将最大值更新为 a_j ，那么前 i-1 项的最大值为 a_k ， k≥1 && k≤pos_j ；

　　显然 ,dp(1,i) = 1 ，则将dp(1,i) 作为 初始状态，递推填表即可。 

代码：

#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int,int> pii;
typedef pair<LL,LL> pLL;
typedef pair<double,double> pdd;
const int N=5e3+5;
const int M=5e3+5;
const int inf=1e8;
const LL mod=998244353;
const double eps=1e-8;
const long double pi=acos(-1.0L);
#define ls (i<<1)
#define rs (i<<1|1)
#define fi first
#define se second
#define pb push_back
#define eb emplace_back
#define mk make_pair
#define mem(a,b) memset(a,b,sizeof(a))
LL read()
{
    LL x=0,t=1;
    char ch;
    while(!isdigit(ch=getchar())) if(ch=='-') t=-1;
    while(isdigit(ch)){ x=10*x+ch-'0'; ch=getchar(); }
    return x*t;

}
LL a[N],dp[N][N],pos[N],sum[N];
int main()
{
    int n=read();
    for(int i=1;i<=n;i++) a[i]=read();
    sort(a+1,a+n+1);
    int l=0;
    for(int i=1;i<=n;i++){
        while(a[l+1]*2<=a[i]) l++;
        pos[i]=l;
    }
    for(int i=1;i<=n;i++) dp[1][i]=1;
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j<=n;j++) sum[j]=(sum[j-1]+dp[i-1][j])%mod;
        for(int j=1;j<=n;j++)
        {
            dp[i][j]=sum[pos[j]];
            dp[i][j]+=dp[i-1][j]*max(0LL,pos[j]-i+2);
            dp[i][j]%=mod;
        }
    }
    printf("%lld
",dp[n][n]);
    return 0;
}