【模板】LCA

（十一集训前最后的挣扎）

先介绍LCA是啥吧。。

LCA：Lowest Common Ancestors（最近公共祖先）

用来求树上任意两点的最近相同父亲节点，有各种不同的方法，这里先介绍树上倍增求LCA（另一种我不会。。）

先看一道题：（RP++）

这是翻译：

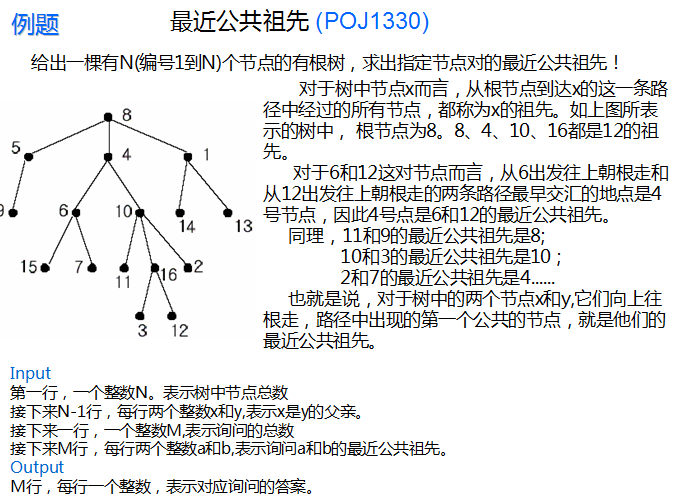
先看看朴素算法：

先依次向上查找x的祖先，存入xa数组，再依次向上查找y的祖先，与xa数组中的值比较，第一个相同的就是x，y的最近公共祖先。

每一次查找的时间复杂度是O（n）

（好慢。。）

而树上倍增就是将查找的次数减少，每一次都尽可能多的往上走，大大减少查找次数。

这里倍增的倍就是指2的多少次方，但是倍增总要有个上限，对于有n层的树，上限就是log_2^n。

流程图（摘自老师的PPT）：

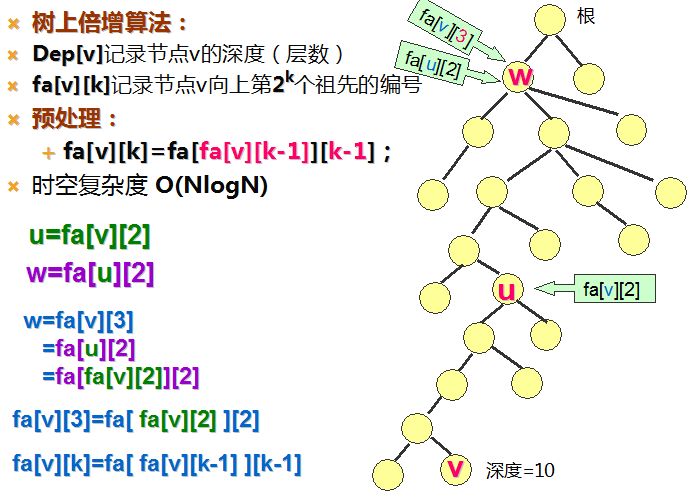
要怎么用代码实现呢。。

先看流程图：

 

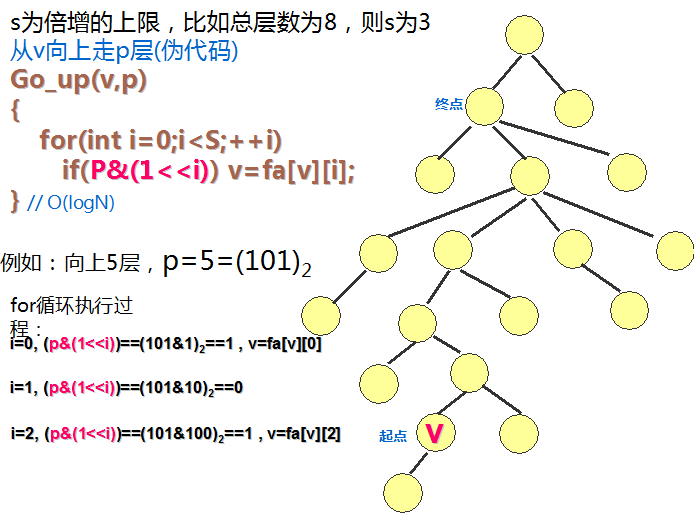
出现了一个令我迷茫的东西----位运算符“&”

这个东西应该怎么用呢？

比如：1010 0011& 0000 1111，结果为0000 0011。也就是与上0相当于把那位数清0，与上1相当于把那位保留。（摘自百度知道）

（有点像快速幂。。）

但是只用单纯的树上倍增真的可以解决这道题吗？

当x，y不在同一层的时候就会有一点难处理。

这时我们可以先让在更深层的x或y先跳到与另一个节点同一层，再利用树上倍增求LCA。

大概思路就是这样。

看看代码？（想看建树的话请看SPFA）

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
const int maxn = 500005;
const int maxe = 1000005;
int n,m,root;

struct line{
    int from,to;
    line(){}//空构造函数 line p; 
    line(int A,int B){
        //构造函数 line L=line(1,2);
        from=A;to=B;
    }
};
line edge[maxe];
int last[maxn],_next[maxe],e; 
//last[x]表示以x为起点的最后一条边（的编号） 
//_next[i]表示与第i条边起点相同的上一条边（的编号） 
void add_edge(int x,int y){
    edge[++e]=line(x,y);
    _next[e]=last[x];
    last[x]=e;
}
int Fa[maxn][35],Dep[maxn];
void dfs(int x,int fa){
    int i,k,y;
    Fa[x][0]=fa;
    Dep[x]=Dep[Fa[x][0]]+1;                       //记录当前节点的深度 
    k=ceil(log(Dep[x])/log(2));                      //x往上倍增的上限 
    for(i=1;i<=k;i++)Fa[x][i]=Fa[Fa[x][i-1]][i-1];  //倍增计算祖先 
    for(int i=last[x];i;i=_next[i]){
        int v=edge[i].to;
        if(v!=fa)dfs(v,x); 
    }
}
int LCA(int x,int y){
    int i,k,s;
    s=ceil(log(n)/log(2));                 //该树倍增最大可能的上限 
    if(Dep[x]<Dep[y])swap(x,y);      //交换x和y的值 
    /////////////x往上走k层，让x与y处于同一层 //////////
    k=Dep[x]-Dep[y];
    for(i=0;i<=s;i++)
        if(k&(1<<i))x=Fa[x][i];
    if(x==y)return x;                     //x==y时，x就是最近公共祖先 
    ///////////////////////////////////////////////////
    s=ceil(log(Dep[x])/log(2));           //计算向上倍增的上限 
    for(i=s;i>=0;i--)
        if(Fa[x][i]!=Fa[y][i]){ x=Fa[x][i]; y=Fa[y][i]; }
    return Fa[x][0];
}

int main(){
    int i,j,k;
    cin>>n>>m>>root;
    for(i=1;i<n;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add_edge(x,y);
        add_edge(y,x);
    }
    dfs(root,0);
    for(i=1;i<=m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d
",LCA(x,y));
    }
        
} 

 关于核心代码的循环过程：

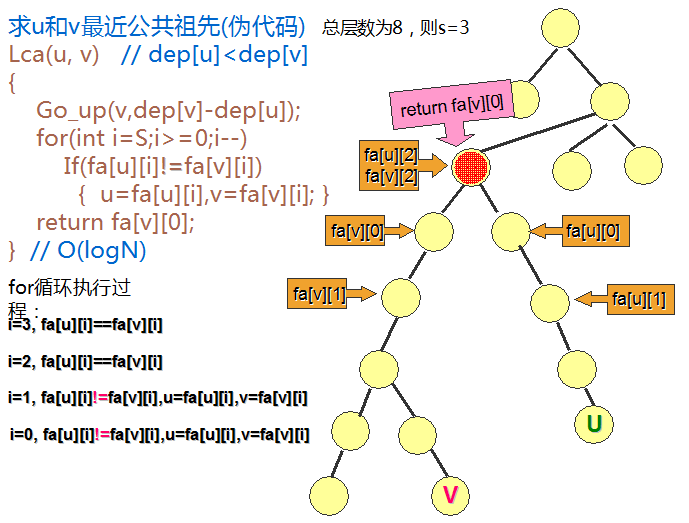
为什么有If(fa[u][i]!=fa[v][i]) { u=fa[u][i],v=fa[v][i]; } 这一句呢？不是当他们相等时就可以结束了吗？

原理：当fa[u][i]==fa[v][i]时，所求的节点不一定是最近的公共祖先。

没有注释的点这里

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
struct edge{
    int next,to;
    edge(){}
    edge(int a,int b)
    {
        next=a;
        to=b;
    }
}e[1000001];
int f[100001][31],dep[100001],first[100001],tot;
void add_edges(int a,int b)
{
 e[++tot]=edge(first[a],b);
 first[a]=tot;
}

void dfs(int x,int fa)
{
    f[x][0]=fa;
    dep[x]=dep[fa]+1;
    int k=ceil(log(dep[x])/log(2));
    for(int i=1;i<=k;i++)
    {
        f[x][i]=f[f[x][i-1]][i-1];
    }
    for(int i=first[x];i;i=e[i].next)
    {
        int pos=e[i].to;
        if(pos!=fa)
        dfs(pos,x);
    }
}
int n,m,root;
int LCA(int x,int y)
{
   if(dep[x]<dep[y])
   swap(x,y);
   int k1=dep[x]-dep[y];
   int k2=ceil(log(n)/log(2));
   for(int i=0;i<=k2;i++)
   {
        if(k1&(1<<i))
        x=f[x][i];
   }
   if(x==y)
   return x;
   int k3=ceil(log(dep[x])/log(2));
   for(int i=k3;i>=0;i--)
   {
      if(f[x][i]!=f[y][i])
      {
           x=f[x][i];y=f[y][i];
        }
    }
    return f[x][0];
}
int main(){
    int i,j,k;
    cin>>n>>m>>root;
    for(i=1;i<n;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add_edges(x,y);
        add_edges(y,x);
    }
    dfs(root,0);
    for(i=1;i<=m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d
",LCA(x,y));
    }
        
} 

（RP++!）