既然没有题解,那么我就来提供给一份。
--
首先我们看到数据范围。妈耶!数据这么大,一开始还想用个DP来做,但是看着就不行,那么根据这个数据范围,我们大致可以猜到这道题的算法是一个贪心,那么我们怎么贪呢?
我们首先还是先画一个图:
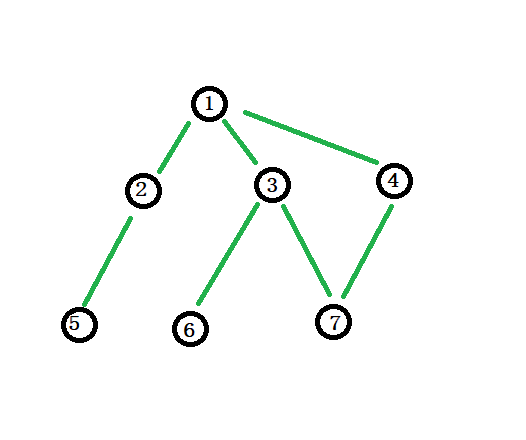
样例解释一下:
我们取的点是(3),(5),(7)。
看到题目,因为(1)号节点的入度为0,那么就一定不能选择(1)号节点,那么接下来可以供我们选择的最大的权值的点也就只有(3),(5),(7)号节点,那么我们就来一个贪心策略:对每一个节点的权值进行排序,然后将所有不能取的节点全部不算,剩下的就都取最大的那几个。
以下是(30)分骗分程序
# include <bits/stdc++.h>
# define Ri register int
# define for1(i,a,b) for(Ri i(a);i<=b;++i)
# define for2(i,a,b) for(Ri i(a);i>=b;--i)
using namespace std;
inline int read ()
{
int w = 0,x = 0;
char ch = 0;
while (!isdigit(ch)) { w |= ch =='-'; ch = getchar();}
while (isdigit(ch)) { x = (x<<1) + (x<<3) + (ch ^ 48); ch = getchar(); }
return w ? -x : x;
}
const int Maxm = 2000004;
const int Maxn = 5000004;
int Nedge, n, m, k;
int head[Maxm], ind[Maxn];
struct node{
int v ,id ,ind ;
}a[5000004];
bool cmp (node a,node b)
{
return a.v > b.v;
}
int main()
{
n = read(),m = read(),k = read(); Nedge = 1;
for1(i ,1 ,n ) a[i].v = read(),a[i].id = i;
for1(i ,1 ,m )
{
int u = read(),v = read();
a[v].ind ++;
}
sort (a + 1 , a + 1 + n , cmp);
int cnt = 0 , ans = 0;
for1(i ,1 ,n)
{
if (a[i].ind == 0) continue;
else
{
ans += a[i].v;
cnt ++;
if (cnt == k) break;
}
}
printf ("%d
", ans);
return 0;
}
但是这个贪心一定是错的。
为什么
我们来想一下,如果可以去掉的节点,是某一个接下来可以取的节点的唯一一个入边来源,那么这个一定会影响后面的答案,这个点也就不取了,所以我们就不能这样做。
那么我们应该怎么做呢?
这个时候我们就需要 胆大心细地思考题目了。我是好好听了出征大会的
其实也就只需要在这个贪心的基础上,加上一个契机,这个契机就是让当前这个删去的点,可以不对后面的点产生影响。
正解策略是:我们首先缩点,然后找到入度为0的环,删去这个环中权值最小的点,然后从小到大排序,取前k大的点。
我们先给一个缩点的模板吧!
inline void tarjan(int u)
{
dfn[u] = low[u] = ++ dep;
vis[u] = 1;
S[top++] = u;
for (int i = head[u]; i != -1; i = edge[i].next )
{
int v = edge[i].to;
if (!dfn[v])
{
tarjan(v);
low[u] = Min(low[u] ,low[v]);
}
else if (vis[v]) low[u] = Min(low[u] ,low[v]);
}
int j;
if (dfn[u] == low[u])
{
sum ++;
do
{
j = S[ -- top];
belong[j] = sum ;
vis [j] = 0;
}while (u != j) ;
}
}
解释
那么我们就需要一个手段,使得这个这个点成为一个删去和不删去,不会影响答案得到东西:这个玩意的名字叫做缩点。
为什么我们会想到缩点,我们得从DAG中的环开始说起。
早在。。因为在有向图中,每一个点都是可以互相到达的,那么所以这个有向图中的每一个点都是有入度的,没有人反驳吧!,所以这个里面的点都是可以随意取的,但是要注意attention:当你这这个环是(0)的入度时,那么你就不能随意取掉最后一个点了,因为你这个最后一个点可能就没有入度了,那么我们为了保证所有的点都可以取到,我们就将这个环内的权值最小的点删去,那么这样就可以保证这个环断开后,这个点集中的点就可以随便取了。
那么还有一个问题,也就是如果是一个节点的缩点?
其实也是一个道理,我就不解释了,也就是把这个点删掉,反正这个点完全没有用。
以下是AC代码(新的码风本人感觉还是挺好看的QAQ)
# include <bits/stdc++.h>
# define Ri register int
# define for1(i,a,b) for(Ri i(a);i<=b;++i)
# define for2(i,a,b) for(Ri i(a);i>=b;--i)
# define ms(a,b) memset(a,b,sizeof(a))
using namespace std;
typedef long long LL;
const int M = 2000005;
struct Edge{
int to ,next;
}edge[M];
int dfn[M], vis[M], low[M], S[M], head[M] ,belong[M] ,ind[M];
int dep, top, sum , n ,m ,k ,Nedge;
struct node{
int v ,id ;
}a[M];
inline int read() //快读
{
int w = 0,x = 0;
char ch = 0;
while (!isdigit(ch))
{
w |= ch == '-';
ch = getchar();
}
while (isdigit(ch))
{
x = (x<<1) + (x<<3) + (ch^48);
ch = getchar();
}
return w ? -x : x ;
}
inline int Min(int n,int m) //三目取min
{
return n < m ? n : m;
}
inline void Add_Edge(int u ,int v) //链式前向星
{
edge[Nedge] = (Edge) {v ,head[u]} ;
head[u] = Nedge++;
}
inline void tarjan(int u) //tarjan缩点模板
{
dfn[u] = low[u] = ++ dep;
vis[u] = 1;
S[top++] = u;
for (int i = head[u]; i != -1; i = edge[i].next )
{
int v = edge[i].to;
if (!dfn[v])
{
tarjan(v);
low[u] = Min(low[u] ,low[v]);
}
else if (vis[v]) low[u] = Min(low[u] ,low[v]);
}
int j;
if (dfn[u] == low[u])
{
sum ++;
do
{
j = S[ -- top];
belong[j] = sum ;
vis [j] = 0;
}while (u != j) ;
}
}
inline bool cmp1(node a,node b) //从小到大排序
{
return a.v < b.v;
}
inline bool cmp2(node a,node b) //从大到小排序
{
return a.v > b.v;
}
int main()
{
ms(head ,-1);
ms(dfn ,0);
ms(vis ,0);
ms(belong ,0);
sum = 0,dep = 0,top = 0;
n = read(),m = read(),k = read();
for1(i ,1 ,n) a[i].v = read(),a[i].id = i;
for1(i ,1 ,m)
{
int u = read(),v = read();
Add_Edge(u , v);
}
for1(i ,1 ,n)
{
if (!dfn[i]) tarjan(i); // 缩一波点
}
for1(i ,1 ,n)
{
for (int j = head[i]; j != -1; j = edge[j].next)
{
int v = edge[j].to;
if ( belong[i] != belong[v] ) ind[belong[v]] ++;
}
}//统计当前缩完点后的每个点的入度
sort(a + 1, a + 1 + n ,cmp1);
for1(i ,1 ,n)
{
if (ind[belong[a[i].id]] == 0)
{
a[i].v = 0;
ind[belong[a[i].id]] = 1;
}
}//删去一个联通块中权值最小的点
sort(a + 1 , a + 1 + n ,cmp2);
LL ans = 0, cnt = 0;
for1(i ,1 ,n) //计算我们的答案
{
ans += a[i].v;
cnt ++ ;
if (cnt == k) break;
}
printf ("%lld
", ans);
return 0;
}