声明:感谢修改这篇博客的dsr
Day 1
先说一下上午的听课吧,哎~,简直了,简直(⊙o⊙)…咋说呢,引人入胜???No! 是昏昏欲睡好吧。。。一点听课欲都没有(强撑....),一上午停下来简直怀疑人生。下午上机,啥??上机居然断网!!!搞啥子嘛,,,于是整理上午的笔记,╮(╯▽╰)╭内心崩溃。
一、同余
知识点:
同余,如果a和b对m取模得到的结果相同,那么说a和b在模m意义下相等,或者说二者同余,记作a≡b (mod m)(其实中间应该是三条杠,但是打不出来),并且就划分为同一类。显然模m意义下一共有m类数字,以0,1,...,m-1为代表元素。注意负数也是可以取模的,例如-1 mod 3 = 2。如果a=km+r(0<=r<m),那么a=r(mod m),这称作”带余除法”。特殊的,如果r=0,那么m是a的因数,a是m的倍数,称为m整除a,记作m|a。
代码实现:

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 using namespace std; 6 typedef long long ll; 7 ll a,b,x,y,z; 8 inline ll read() { 9 ll n=0,f=1;char ch=getchar(); 10 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 11 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 12 return n*f; 13 } 14 inline void gcd(ll a,ll b) { 15 if(!b) { 16 x=1,y=0; 17 return ; 18 } 19 gcd(b,a%b); 20 z=x,x=y; 21 y=z-a/b*y; 22 } 23 int main() { 24 a=read(),b=read(); 25 gcd(a,b); 26 printf("%lld\n",(x+b)%b); 27 return 0; 28 }
二、因数
知识点:
刚才说了,如果a|b,也就是a整除b,那么b是a的倍数,a是b的因数。显然如果a|b,a|c,那么a|(b±c),a|(bx+cy),即a整除b和c的线性组合最大公因数gcd(a,b),或者简写成(a,b),定义为,最大的d,满足d|a且d|b。显然d|(a,b)等价于,d|a且d|b另一个很显然的是,(a,b)=(a+b,b)=(a-b,b)=(a mod b,b)特别的,如果(a,b)=1,那么称作a和b互质最小公倍数[a,b]同理。二者关系:[a,b]=ab/(a,b),注意只对两个数字恒有效。
三、欧拉定理

四、逆元

Exgcd 求逆元 代码实现:

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 using namespace std; 5 typedef long long ll; 6 ll a,b,x,y,z,n,mod; 7 inline ll read() { 8 ll n=0,f=1;char ch=getchar(); 9 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 10 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 11 return n*f; 12 } 13 inline void exgcd(ll a,ll b,ll &x,ll &y) { 14 if(!b) { 15 x=1,y=0; 16 return ; 17 } 18 exgcd(b,a%b,x,y); 19 z=x,x=y; 20 y=z-a/b*y; 21 } 22 int main() { 23 n=read(),mod=read(); 24 exgcd(n,mod,x,y); 25 x=(x%mod+mod)%mod; 26 printf("%lld\n",x); 27 return 0; 28 }
线性求逆元 代码实现:

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 using namespace std; 6 typedef long long ll; 7 const int N=3e6+10; 8 inline int read() { 9 int n=0,f=1;char ch=getchar(); 10 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 11 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 12 return n*f; 13 } 14 int n,p,a[N]; 15 int main(){ 16 n=read(),p=read(); 17 a[0]=a[1]=1; 18 for(int i=2;i<=n;++i) a[i]=a[i]-(ll)(p/i)*a[p%i]%p; 19 for(int i=1;i<=n;++i) { 20 if(a[i]<0) a[i]+=p; 21 printf("%d\n",a[i]); 22 } 23 return 0; 24 }
五、扩展欧拉定理

六、卢卡斯定理

代码实现:

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 typedef long long ll; 8 const int N=1e5+10; 9 int n,m,p,k; 10 ll a[N],b[N]; 11 inline int read() { 12 int n=0,f=1;char ch=getchar(); 13 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 14 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 15 return n*f; 16 } 17 inline ll lucas(int x,int y) { 18 if(x<y) return 0; 19 else if(x<p) return b[x]*a[y]*a[x-y]%p; 20 else return lucas(x/p,y/p)*lucas(x%p,y%p)%p; 21 } 22 int main() { 23 k=read(); 24 while (k--) { 25 n=read(),m=read(),p=read(); 26 a[0]=a[1]=b[0]=b[1]=1; 27 for(int i=2;i<=n+m;++i) b[i]=b[i-1]*i%p; 28 for(int i=2;i<=n+m;++i) a[i]=(p-p/i)*a[p%i]%p; 29 for(int i=2;i<=n+m;++i) a[i]=a[i-1]*a[i]%p; 30 printf("%lld\n",lucas(n+m,m)); 31 } 32 return 0; 33 }
七、GCD/EXGCD
代码实现:

1 inline void exgcd(ll a,ll b,ll &x,ll &y) { 2 if(!b) { 3 x=1,y=0; 4 return ; 5 } 6 exgcd(b,a%b,x,y); 7 z=x,x=y; 8 y=z-a/b*y; 9 }
青蛙的约会:

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 typedef long long ll; 7 const int N=100000010; 8 ll x,y,m,n,l,a,b,js,mod; 9 10 inline ll read() { 11 ll n=0,f=1;char ch=getchar(); 12 while (ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} 13 while (ch>='0'&&ch<='9') {n=n*10+ch-'0';ch=getchar();} 14 return n*f; 15 } 16 17 inline ll gcd(ll a,ll b) { 18 if(b) return gcd(b,a%b); 19 else return a; 20 } 21 22 inline void IU(ll a,ll b,ll &x,ll &y) { 23 if(!b) { 24 x=1,y=0; 25 return ; 26 } 27 IU(b,a%b,y,x); 28 y-=a/b*x; 29 } 30 31 inline void pd() { 32 if((b-a)%js) printf("Impossible\n"); 33 else { 34 x=(x*((b-a)/js)%mod+mod)%mod; 35 printf("%lld\n",x); 36 } 37 } 38 39 int main() { 40 a=read(),b=read(),m=read(),n=read(),l=read(); 41 js=gcd(m-n,l); 42 mod=abs(l/js); 43 IU(m-n,l,x,y); 44 pd(); 45 return 0; 46 }
八、关于二元一次不定方程
知识点(Zz..摘自度娘):
使二元一次方程两边相等的一组未知数的值,叫做二元一次方程的一个解.
对二元一次方程的解的理解应注意以下几点:
①一般地,一个二元一次方程的解有无数个,且每一个解都是指一对数值,而不是指单独的一个未知数的值;
②二元一次方程的一个解是指使方程左右两边相等的一对未知数的值;反过来,如果一组数值能使二元一次方程左右两边相等,那么这一组数值就是方程的解;
③在求二元一次方程的解时,通常的做法是用一个未知数把另一个未知数表示出来,然后给定这个未知数一个值,相应地得到另一个未知数的值,这样可求得二元一次方程的一个解.
折叠注意点:
(1)二元一次方程组:由两个二元一次方程所组成的一组方程,叫做二元一次方程组.
(2)二元一次方程组的解:二元一次方程组中两个方程的公共解,叫做二元一次方程组的解.
对二元一次方程组的理解应注意:
①方程组各方程中,相同的字母必须代表同一数量,否则不能将两个方程合在一起.
②怎样检验一组数值是不是某个二元一次方程组的解,常用的方法如下:将这组数值分别代入方程组中的每个方程,只有当这组数值满足其中的所有方程时,才能说这组数值是此方程组的解,否则,如果这组数值不满足其中任一个方程,那么它就不是此方程组的解.
九、CRT
知识点:
定理1:几个数相加,如果存在一个加数,不能被整数a整除,那么它们的和,就不能被整数a整除。
定理2:两数不能整除,若除数扩大(或缩小)了几倍,而被除数不变,则其商和余数也同时扩大(或缩小)相同的倍数(余数必小于除数)。
代码实现:

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 using namespace std; 6 typedef long long ll; 7 ll m[15],a[15]; 8 int n; 9 inline ll read() { 10 ll n=0,f=1;char ch=getchar(); 11 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 12 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 13 return n*f; 14 } 15 inline int fread() { 16 int n=0,f=1;char ch=getchar(); 17 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 18 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 19 return n*f; 20 } 21 inline void gcd(ll a,ll b,ll &d,ll &x,ll &y) { 22 if(!b){ 23 d=a; 24 x=1,y=0; 25 } else{ 26 gcd(b,a%b,d,y,x); 27 y-=(a/b)*x; 28 } 29 } 30 inline ll work_(int n,ll *m,ll *a) { 31 ll p=1,d,y,x=0; 32 for(int i=0;i<n;++i) p*=m[i]; 33 for(int i=0;i<n;++i){ 34 ll w=p/m[i]; 35 gcd(m[i],w,d,d,y); 36 x=(x+y*w*a[i])%p; 37 } 38 return (x+p)%p; 39 } 40 int main() { 41 n=fread(); 42 for(int i=0;i<n;++i) m[i]=read(),a[i]=read(); 43 printf("%lld",work_(n,m,a)); 44 }
十、扩展欧几里得

十一、线性筛
知识点:
可以在O(n)时间内筛出1~n的所有质数。如果F(n)是个积性函数,根据定义我们只要能够低于O(lgn)的知道每个F(p^c)的值,我们就能在O(n)时间内求出F(1)~F(n)。具体做法是这样的,每次枚举一个数字i,枚举所有已经筛出来的1~i中的质数k,那么x=ik不是质数,并且k是x的最小质因子。如果i%k==0,就break掉k的循环。可以证明每个数字都只会被其最小的质因子筛去,同时利用这个性质可以顺便筛出一些积性函数。这样你可以维护每个数字的最小质因子lp[n],最小质因子对应的那个若干次方lpc[n],这样对于积性函数每次只要计算满足lpc[n]=n的那些F[n],然后用积性函数的性质就可以维护1~n的F。
代码实现:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 const int N=10000010; 6 int n,m,x; 7 bool vis[N]={1,1}; 8 int a[N]; 9 inline int read() { 10 int n=0,f=1;char ch=getchar(); 11 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 12 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 13 return n*f; 14 } 15 // 1 16 inline void ss(int n,int m) { 17 for(int i=2;i*i<=n;++i) 18 if(!vis[i]) 19 for(int j=i*i;j<=n;j+=i) vis[j]=true; 20 while(m--) { 21 x=read(); 22 if(vis[x]) printf("No\n"); 23 else printf("Yes\n"); 24 } 25 return; 26 } 27 // 2 28 inline void IU(int n,int m) { 29 int js=0; 30 for(int i=2;i<=n;++i) { 31 if(!vis[i]) a[++js]=i; 32 for(int j=1;j<=js&&i*a[j]<=n;++j) { 33 vis[i*a[j]]=true; 34 if(i%a[j]==0) break; 35 } 36 } 37 while(m--) { 38 x=read(); 39 if(vis[x]) printf("No\n"); 40 else printf("Yes\n"); 41 } 42 } 43 int main() { 44 n=read(),m=read(); 45 //ss(n,m); 46 IU(n,m); 47 return 0; 48 }
十二、BSGS
知识点:
bsgs算法,又称大小步算法(某大神称拔山盖世算法)或北上广深算法。
主要用来解决 A^x=B(mod C)(C是质数),都是整数,已知A、B、C求x。
代码实现(poj 2417):

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<map> 6 using namespace std; 7 typedef long long ll; 8 map<ll,int> q; 9 ll p,m,n,a,b,z,ans,t,bz; 10 inline ll fpow(ll x) { 11 ll s=1,res=a; 12 while (x>0) { 13 if(x&1) s=(s*res)%p; 14 x=x>>1; 15 res=(res*res)%p; 16 } 17 return s; 18 } 19 int main() { 20 while (scanf("%lld%lld%lld",&p,&a,&b)!=EOF) { 21 if(a%p==0) { 22 printf("no solution\n"); 23 continue; 24 } 25 q.clear(); 26 m=ceil(sqrt(p)); 27 bz=0,z=b%p,q[z]=0; 28 for(int i=1;i<=m;++i) z=(z*a)%p,q[z]=i; 29 t=fpow(m); 30 z=1; 31 for(int i=1;i<=m;++i) { 32 z=(z*t)%p; 33 if(q[z]) { 34 bz=1; 35 ans=i*m-q[z]; 36 printf("%lld\n",(ans%p+p)%p); 37 break; 38 } 39 } 40 if(!bz) printf("no solution\n"); 41 } 42 return 0; 43 }
十三、莫比乌斯反演
知识点:(摘自度娘~~)
数论函数,就是正整数映射到非负整数的函数。积性函数,如果一个数论函数f满足对于任意(x,y)=1,有f(xy)=f(x)f(y),那么称f是积性函数。显只要知道了所有的f(p^c)就可以知道所有的f(n)完全积性函数,如果一个数论函数满足对于任意x和y,都有f(xy)=f(x)f(y),那么称f是完全积性函数
性质:
性质一(莫比乌斯反演公式): 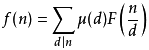
性质二:μ(n)是积性函数
性质三:设f是算术函数,它的和函数 
是积性函数,那么 f 也是积性函数。
莫比乌斯反演定理:
设f(n) 和g(n) 是定义在正整数集合上的两个函数,定义如下。

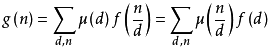
则 
证明:(摘自度娘~)
充分性证明:
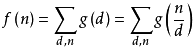
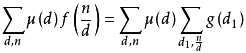

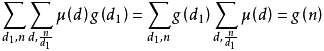
考虑到:

因此
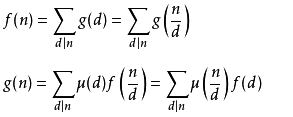
必要性证明:
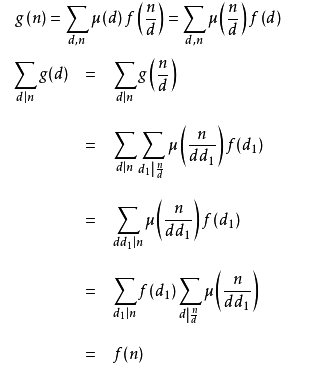
考虑到:

因此

证明2:



例题:
问题描述
给定5个整数:a, b, c, d, k,你要在a中找到x。在c b,y…即GCD(x, y) = k, GCD(x, y)表示x和y的最大公约数,由于选项的数量可能很大,所以只需要输出不同的数对的总数。请注意,(x=5, y=7)和(x=7, y=5)被认为是相同的。
输入
输入由几个测试用例组成。输入的第一行是案例的数量。不超过3000例。
每一种情况包含五个整数:a、b、c、d、k、0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000,如上所述。
输出
对于每个测试用例,打印选项的数量。使用示例中的格式。
样例输入
2
1 3 1 5 1。
1 11014 1 14409 9
样例输出
案例1:9
案例2:736427
代码实现:

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<map> 6 using namespace std; 7 typedef long long ll; 8 const int N=1e5+10; 9 int v[N],a[N],b[N]; 10 int n,m,js,jc,x,y,z,k; 11 ll res,ans; 12 inline int read() { 13 int n=0,f=1;char ch=getchar(); 14 while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();} 15 while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();} 16 return n*f; 17 } 18 int main() { 19 b[1]=1; 20 for(int i=2;i<=100000;++i) { 21 if(!v[i]) a[++js]=i,b[i]=-1; 22 for(int j=1;j<=js;++j) { 23 int k=a[j]*i; 24 if(k>100000) break; 25 v[k]=1; 26 if(i%a[j]==0) { 27 b[k]=0; 28 break; 29 } else b[k]=-b[i]; 30 } 31 } 32 k=read(); 33 while(k--) { 34 ++jc; 35 res=ans=0; 36 n=read(),m=read(),x=read(),y=read(),z=read(); 37 if(!z) { 38 printf("Case %d: 0\n",jc); 39 continue; 40 } 41 m/=z;y/=z; 42 if(m>y) swap(m,y); 43 for(int i=1;i<=m;++i) res+=(ll)b[i]*(m/i)*(y/i); 44 for(int i=1;i<=m;++i) ans+=(ll)b[i]*(m/i)*(m/i); 45 printf("Case %d: %lld\n",jc,res-ans/2); 46 } 47 return 0; 48 }
十四、狄利克雷卷积

十五、数论分块

