20200704联考T2 B

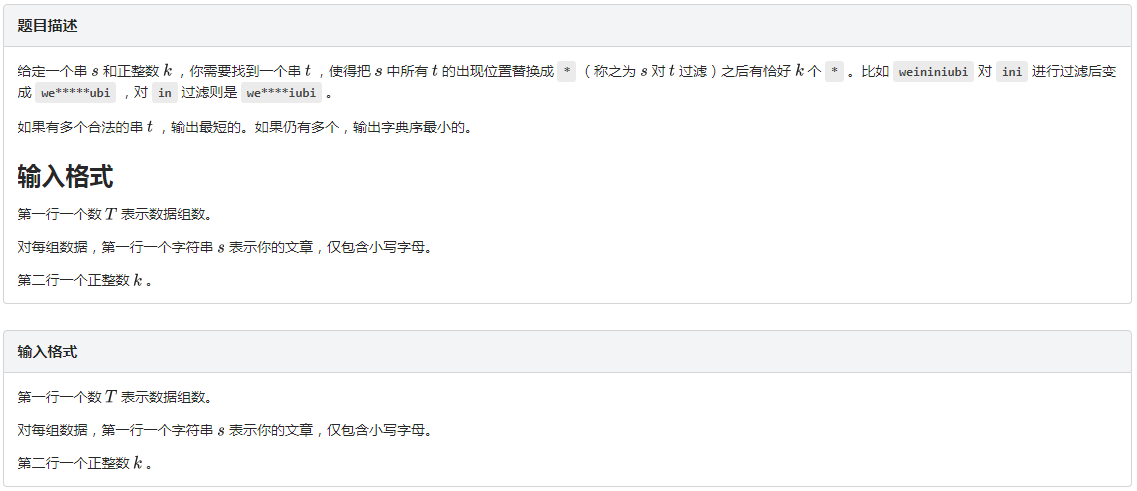
题目描述：

分析：
建立后缀自动机，对于同一节点上的子串，由于endpos集合相同，覆盖的大小必定随长度的增加单调不降
维护endpos集合相邻两个位置的距离，二分+线段树可以快速算出长度为(mid)的子串覆盖的大小
在后缀树上从下往上合并，两个位置的距离用set维护，在线段树上修改
线段树合并，set合并，用启发式合并
最后子串字典序最小可以再写一发后缀数组，我是使用的暴力判断，可能的位置与答案长度的乘积不会很大（大雾）
时间复杂度(O(nlog^2n))

#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<algorithm>
#include<queue>
#include<map>
#include<set>

#define maxn 50005
#define INF 0x3f3f3f3f

using namespace std;

inline int getint()
{
	int num=0,flag=1;char c;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
	while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
	return num*flag;
}

int n,K;
struct node{
	int fa,nxt[26],len;
}t[maxn];
int lst,tot,cur;
char s[maxn];
int rt[maxn],lc[maxn<<5],rc[maxn<<5],sz[maxn<<5],sum[maxn<<5];
int fir[maxn],nxt[maxn],to[maxn],cnt;
set<int>S[maxn];
int P[maxn];
vector<int>V;
int id[maxn];
int ans;
int L,R;

inline void newnode(int u,int v)
{to[++cnt]=v,nxt[cnt]=fir[u],fir[u]=cnt;}
inline void insert(int c)
{
	int p=lst,np=lst=++tot;
	t[np].len=t[p].len+1;
	while(p&&!t[p].nxt[c])t[p].nxt[c]=np,p=t[p].fa;
	if(!p)t[np].fa=1;
	else
	{
		int q=t[p].nxt[c];
		if(t[q].len==t[p].len+1)t[np].fa=q;
		else
		{
			int nq=++tot;
			memcpy(t[nq].nxt,t[q].nxt,sizeof t[q].nxt);
			t[nq].fa=t[q].fa,t[nq].len=t[p].len+1;
			t[q].fa=t[np].fa=nq;
			while(p&&t[p].nxt[c]==q)t[p].nxt[c]=nq,p=t[p].fa;
		}
	}
}

inline void update(int &i,int l,int r,int p,int op)
{
	if(!i){i=++cur;lc[i]=rc[i]=sum[i]=sz[i]=0;}
	sz[i]+=op,sum[i]+=op*p;
	if(l==r)return;
	int mid=(l+r)>>1;
	if(p<=mid)update(lc[i],l,mid,p,op);
	else update(rc[i],mid+1,r,p,op);
}
inline int getsum(int i,int l,int r,int ql,int qr)
{
	if(!i||r<ql||qr<l)return 0;
	if(ql<=l&&r<=qr)return sum[i];
	int mid=(l+r)>>1;
	return getsum(lc[i],l,mid,ql,qr)+getsum(rc[i],mid+1,r,ql,qr);
}
inline int getsz(int i,int l,int r,int ql,int qr)
{
	if(!i||r<ql||qr<l)return 0;
	if(ql<=l&&r<=qr)return sz[i];
	int mid=(l+r)>>1;
	return getsz(lc[i],l,mid,ql,qr)+getsz(rc[i],mid+1,r,ql,qr);
}

inline void solve(int u,int v)
{
	if(S[u].size()<S[v].size())swap(rt[u],rt[v]),swap(S[u],S[v]);
	while(!S[v].empty())
	{
		int p=*(S[v].begin());S[v].erase(p);
		S[u].insert(p);
		set<int>::iterator it1,it2,it3;
		it1=it2=it3=S[u].find(p);
		it2--,it3++;
		if(it1==S[u].begin())update(rt[u],1,n,*it3-*it1,1);
		else if(it3==S[u].end())update(rt[u],1,n,*it1-*it2,1);
		else update(rt[u],1,n,*it3-*it2,-1),update(rt[u],1,n,*it1-*it2,1),update(rt[u],1,n,*it3-*it1,1);
	}
}

inline int getans(int u,int L)
{return getsum(rt[u],1,n,1,L)+getsz(rt[u],1,n,L+1,n)*L+min(*(S[u].begin()),L);}

inline void dfs(int u)
{
	for(int i=fir[u];i;i=nxt[i])
	{
		dfs(to[i]),solve(u,to[i]);
		if(!P[u])P[u]=P[to[i]];
	}
	if(u!=1)
	{
		int l=t[t[u].fa].len+1,r=t[u].len,num=INF;
		while(l<=r)
		{
			int mid=(l+r)>>1;
			int tmp=getans(u,mid);
			if(tmp==K){num=mid;break;}
			if(tmp>K)r=mid-1;
			else l=mid+1;
		}
		if(num<ans)ans=min(ans,num),V.clear();
		if(num==ans)V.push_back(u);
	}
}

inline void getS()
{
	for(int k=0;k<V.size();k++)
	{
		int u=V[k];
		int l=P[u]-ans+1,r=P[u];
		if(!L)L=l,R=r;
		else
		{
			for(int i=0;i<ans;i++)
			{
				if(s[l+i]<s[L+i]){L=l,R=r;break;}
				if(s[l+i]>s[L+i])break;
			}
		}
	}
}

int main()
{
	int T=getint();
	while(T--)
	{
		lst=tot=1,cur=0;ans=INF;L=R=0;
		memset(fir,0,sizeof fir);cnt=0;
		memset(t,0,sizeof t),memset(rt,0,sizeof rt);
		memset(P,0,sizeof P);
		scanf("%s",s+1);
		n=strlen(s+1),K=getint();
		for(int i=1;i<=n;i++)insert(s[i]-'a'),id[i]=lst,S[lst].insert(i);
		for(int i=2;i<=tot;i++)newnode(t[i].fa,i);
		for(int i=1;i<=n;i++)P[id[i]]=i;
		dfs(1);
		for(int i=1;i<=tot;i++)S[i].clear();
		if(ans==INF)printf("NOTFOUND!
");
		else
		{
			getS();s[R+1]=0;
			puts(s+L);
		}
		V.clear();
	}
}