
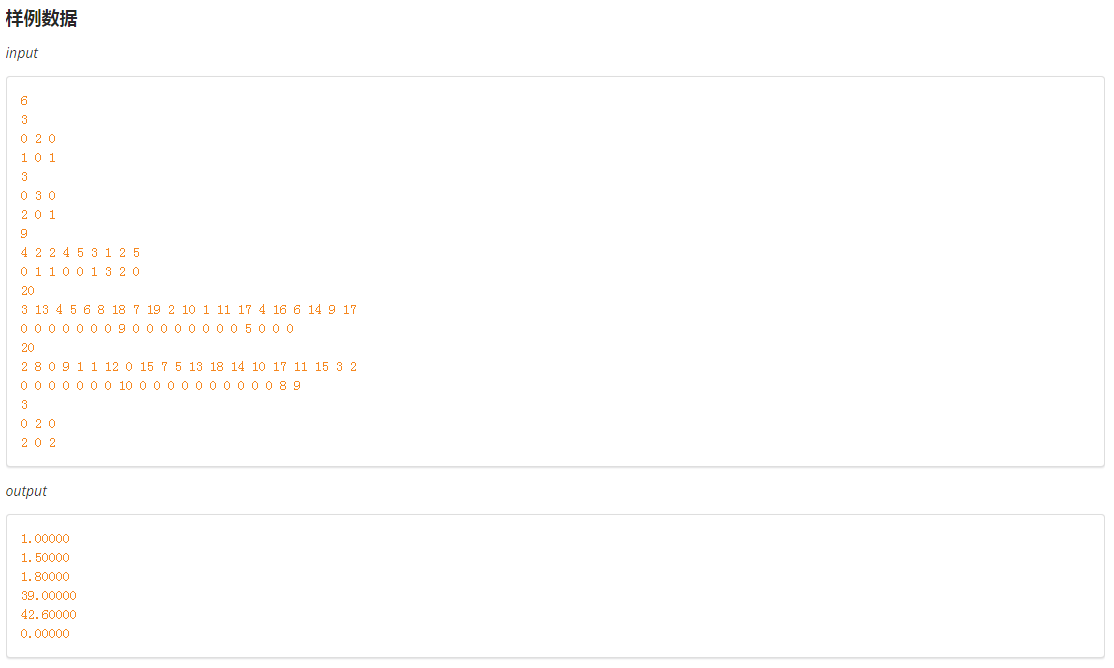

分析:
考虑最终所有水所在的区间,左右两边的土就挖成前缀最小值
假设区间是([l,r]),第一步即可省略,只需要考虑区间内部的情况。可以发现,最小化挖掉的土的体积就是最大化水
的高度,而且显然如果确定了水的高度,那么挖掉这个高度以上的所有的土,就可以求出这个高度以下最多可以放多
少体积的水。如果水多了,说明水的高度还可以更高,否则说明水的高度必须降低。因此二分水的高度就可以确定最
终的水高度。
注意到对于一个([l,r]),它的高度“分界”只有((r-l+1))个,即为每个(h)。在相邻两个分界之间,答案随水位变化是一
个一次函数,可以直接除法。所以只需要对分界处进行二分。
发现从([l,r])变成([l,r+1])水位不会上升,所以使用扫描线进行这个过程,复杂度变成了(O(n^2))
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#define maxn 5005
#define INF 0x3f3f3f3f
using namespace std;
inline long long getint()
{
long long num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
int n;
int w[maxn],s[maxn],ml[maxn],mr[maxn],sl[maxn],sr[maxn],S[maxn];
int cnt[maxn];
int main()
{
int T=getint();
while(T--)
{
n=getint();
for(int i=1;i<=n;i++)S[i]=S[i-1]+(s[i]=getint());
s[0]=s[n+1]=INF;
for(int i=1;i<=n;i++)w[0]+=w[i]=getint();
int lpos,rpos;
for(int i=1;i<=n;i++)if(w[i])
{
ml[lpos=i]=s[i];
for(int j=i+1;j<=n+1;j++)ml[j]=min(ml[j-1],s[j]);
for(int j=i+1;j<=n+1;j++)sl[j]=sl[j-1]-ml[j]+s[j];
break;
}
for(int i=n;i;i--)if(w[i])
{
mr[rpos=i]=s[i];
for(int j=i-1;~j;j--)mr[j]=min(mr[j+1],s[j]);
for(int j=i-1;~j;j--)sr[j]=sr[j+1]-mr[j]+s[j];
break;
}
double ans=1e18;
for(int l=1;l<=n;l++)
{
memset(cnt,0,sizeof cnt);
int h=1000,down=0,cw=0;
for(int r=l;r<=n;r++)
{
if(s[r]<=h)
{
down+=h-s[r],cnt[s[r]]++,cw++;
while(down>w[0])down-=cw-=cnt[h--];
}
double res=0;
int lh=s[l-1],rh=s[r+1];
if(lpos<l)res+=sl[l],lh=ml[l-1];
if(rpos>r)res+=sr[r],rh=mr[r+1];
double x=h+1.0*(w[0]-down)/cw;
res+=(S[r]-S[l-1])-(r-l+1)*x+w[0];
if(x>min(lh,rh))res+=(x-min(lh,rh))*(r-l+1);
ans=min(ans,res);
}
}
printf("%.5f
",ans);
memset(w,0,sizeof w);memset(ml,0,sizeof ml),memset(mr,0,sizeof mr),memset(sl,0,sizeof sl),memset(sr,0,sizeof sr);
}
}
