【题目描述】
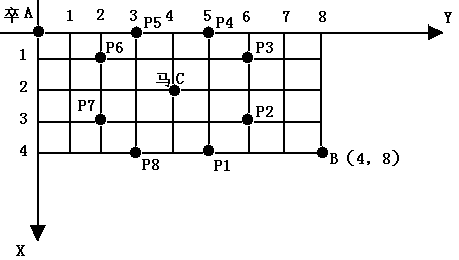
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上的某一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点,如图3-1中的C点和P1,……,P8,卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的,C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。
【输入】
给出n、m和C点的坐标。
【输出】
从A点能够到达B点的路径的条数。
【输入样例】
8 6 0 4
【输出样例】
1617
例题不怎么详的解:
过河卒,中国象棋用语,过了河的卒可以向前、向左、向右移动,但是单单不能后退的,所以被广泛用来形容‘没有退路’。
也指的一种只能前进不能后退的破釜沉舟的勇气,或者是指做事小心谨慎步步为营的一种人生态度。
分析:本题中,卒只能向下和右移动,而不能往回走或往左走。可以很快看出,本题可以用搜索来做。但是根据书上来说,好像无法承受较大的数据规模。
以后学完动态规划来把动规算法补上。
用递推的方法,我们可以用一个数组储存到某一点的路径总数,另一个数组(bool型)储存整张棋盘,来代表某个位置马是否能够到达。
假设用F[I,J]到达点(I,J)的路径数目用G[I,J]表示点(I,J)是否为对方马的控制点,G[I,J]=0表示不是对放马的控制点,G[I,J]=1表示是对方马的控制点。
那么有隐含条件:
F[I,J]=0{G[I,J]=1};
根据题目,可以看出卒要从左上到右下,那么只能以向下走和向右走的方法到达终点。换句话说,以逆推的思想,棋盘上的每一个点只能从这个点的左边或者上边到达,由此判断,如果在棋盘上面和左边的边缘上有马可以达到的位置,那么从这个点往后的剩下的整行或整列,卒都不能到达。
而且,从题目来看,这个卒的行走路径还具有很强的不可逆性,无法回头,很容易注意到,棋子每向右走一步,那么它上一步所在的位置的整列(colum)都将无法到达,得出递推关系式:
F[0,J]=F[0,J-1]{J>0,G[0,J]=0};
同理,棋子每向下走一步,那么踏上一步所在位置的整行(row)都将无法到达,则有递推关系式:
F[I,0]=F[I-1,0]{I>0,G[I,0]=0};
这两个关系式都可以看作是用来排除不可能条件的,对真正得出答案没用,缺少了一个核心递推式。
要让程序进行下去,最关键的关系式:
F[I,J]=F[I-1,J]+F[I,J-1]{I>0,J>0,G[I,J]=0};
这里很容易看明白,[i-1][j-1]代表的就是目前点[i,j]左边的点和上面的点总共的可到达路径条数,很明显,其总和就是该点的有效路径。
从一开始的很容易看出来的递推边界开始递推:
F[0,0]=1;
即可得出答案。(哎,第一篇写的就这么麻烦,不过挺清楚的。)
样例代码如下:
#include<iostream>
#include<cstring>
using namespace std;
long long a[30][30];
int vis[30][30];
int next[][2]={{2,1},{1,2},{-1,2},{-2,1},{-2,-1},{-1,-2},{1,-2},{2,-1}};
int main()
{
int n,m;
int x,y;
int nx,ny;
int i,j;
memset(vis,0,sizeof(vis));
cin>>n>>m>>x>>y;
a[0][0]=0;//处理A=B的情况
vis[x][y]=1;//设置马管辖的位置
a[x][y]=0;
for(i=0;i<8;i++)
{
nx=x+next[i][0];
ny=y+next[i][1];
if(0<=nx&&nx<=n&&0<=ny&&ny<=m)
{
vis[nx][ny]=1;
a[nx][ny]=0;
}
}
for(i=0;i<=n;i++)
{
if(vis[i][0]==1)
while(i<=n)
{
i++;
a[i][0]=0;
}
else
a[i][0]=1;
}
for(j=0;j<=m;j++)
{
if(vis[0][j]==1)
while(j<=m)
{
j++;
a[0][j]=0;
}
else
a[0][j]=1;
}
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
if(vis[i][j]==0)
a[i][j]=a[i][j-1]+a[i-1][j];
cout<<a[n][m]<<endl;
return 0;
}
2019-01-28 11:51:23
转载请联系作者