本来是继续加强最短路的训练,但是遇到了一个最短路 + 最大流的问题,最大流什么鬼,昨天+今天学习了一下,应该对ek算法有所了解,凭借学习后的印象,自己完成并ac了这个最大流的模板题
题目大意:都是图论,只是这个图给你的关系是网络关系,就是从s到t的路上,你运送的东西的量必须满足所有路径的限制,而题目给出的就是限制,我们用一个二维数组c存储i到j这一条边的总限制,注意的是,初始化c数组为0,然后增加限制,而不是赋值,因为可能有多条路,但管他几条路呢,只要能运过去走那条都行,所以合并增值
int main()
{
while(~scanf("%d%d",&m,&n))
{
int a,b,x;
memset(c,0,sizeof(c));//最初肯定是不能通过流量
while(m--)
{
scanf("%d%d%d",&a,&b,&x);
c[a][b] += x;//多条路的情况合并为其流量总限制即可
}
int ret = ek(1,n);
printf("%d
",ret);
}
return 0;
}
接下来是ek算法,他的主要思想就是反向边的维护,因为让求最大流只用bfs,dfs求出的所有结果不一定是最优最大的结果,但是我们可以先用bfs进行尝试,但是尝试完这一条路后,我们根据这条路建立一个反向的路,反向路可行表示的结果就是,这一条路被抵消了
引入一下图文解释
下面是所有最大流算法的精华部分:引入反向边
为什么要有反向边呢?
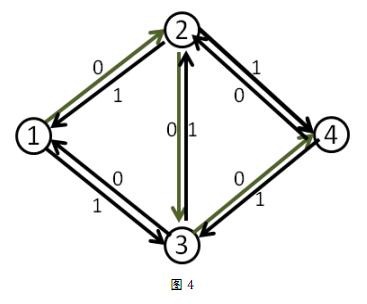
我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量)
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。
那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会
第一个隆重登场的算法是 EK(Edmond—Karp)算法
感谢http://www.cnblogs.com/zsboy/archive/2013/01/27/2878810.html 的博文,里面有很详细的我要给出的第一个代码的模板和对于该算法的深刻理解
其实你看看3为什么要走那条反向路,是因为第一条路1 - 2 - 4把3 - 4 占用了,那么我只能1 - 3 - 2走它的反向路,并尝试走到终点4,如果能走到终点4,那么就代表最终可行线路是1 - 2 - 4和 1 - 3 - 4 ,很想匈牙利的二分图匹配啊,我觉得这么可以理解,就是1 - 3一旦走了反向路就代表他在为1 - 2 寻找另一条不是1 - 2 - 3 - 4 的路线,如果找到了 1 - 2 - 4确定可以走的通,而原来的正向路也能保证1 3 4可以走的通,所以路线就能有化成1 2 4 和1 3 4,如果找不到就不会有任何变化(真的很闲匈牙利啊~~--.--)
所以我们要些bfs,是用来尝试连接1 - n ,并且连接成功返回该线路的最大流,连接失败返回一个flag传到ek算法里
所以在bfs中我们有一个f【i】数组表示从点1到i的最大流,和pre数组,记录该线路的前驱,为ek算法建立反向边做准备
int bfs(int s,int t)
{
memset(pre,-1,sizeof(pre));
f[s] = inf;
queue<int> q;
while(q.size())q.pop();
q.push(s);
while(q.size())
{
int now = q.front();q.pop();
for(int i = 1;i <= n;i++)
{
if(c[now][i] > 0 && pre[i] == -1)
{
pre[i] = now;
f[i] = min(f[now],c[now][i]);
q.push(i);
}
}
}
if(pre[t] == -1)return -1;
return f[t];
}
上面的代码:pre数组还被用来做一个访问标记vis数组
然后就是ek算法建立反向边的问题了,其实就是利用bfs传回的值,对二维数组c进行的增值和减值的操作
int ek(int s,int t)
{
int ret = 0;
while(1)
{
int delta = bfs(s,t);
if(delta == -1)break;
int now = t;
while(now != s)
{
c[pre[now]][now] -= delta;
c[now][pre[now]] += delta;
now = pre[now];
}
ret += delta;
}
return ret;
}
————————————————————————————————————————————————————————————
加油!