马尔可夫随机场 - 条件独立性
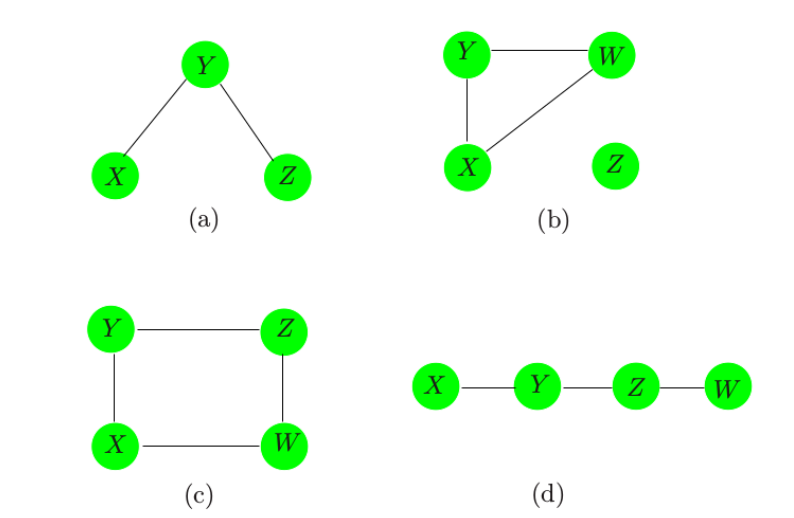
如图,显示了无向图的四个例子。图(G)包含数据对((V,E)),其中(V)是顶点的集合,(E)为边的集合。在马尔可夫网络中,每个顶点表示一个随机变量,顶点之间的边表示两个变量之间的依赖关系,两个顶点之间缺失边表示条件独立。如图((a))中,在给定(Y)的情况下,(X)和(Z)是独立的。在图((b))中,(Z)与(X,Y,W)中的每一个都是独立的。
假设我们有图(G),它的顶点集合(V)表示联合分布为(P)的随机变量集。在马尔可夫图(G)中,某条边的缺失表示在给定其他顶点的变量时,对应的随机变量是条件独立的。
成对马尔可夫性质
设(u)和(v)是无向图(G)中任意两个没有边连接的结点(也就是说两个之间没有依赖的关系),结点(u)和(v)分别对应随机变量(Y_u)和(Y_v)。其他所有结点为(O),对应的随机变量组是(Y_O)。则成对马尔可夫性的表达式如下:
上式的意思是在给定随机变量组(Y_o)的条件下,随机变量(Y_u)和(Y_v)是条件独立的。如图((a))中,在给定(Y)的观测值下,(X)和(Z)是独立的。
局部马尔可夫性质
设(v)是无向图(G)中的任意结点,(W)是与(v)有边连接的所有结点,(O)是(v,W)以外的所有结点(相当于(W)将(v)和(O)给隔开了)。则在给定(W)的条件下,(v)和(O)之间是相互独立的,表达式如下:
在具有正分布的马尔可夫网络中,局部马尔可夫性质和成对马尔可夫性质实质是等价的。
全局马尔可夫性质
如果(A,B)和(C)为子图,且若(A)和(B)的任一路径都交于(C)中的顶点,则称(C)分离(A)和(B)。举个栗子,(Y)分离图((a))和((d))中的(X)和(Z),并且(Z)分离((d))中的(Y)个(W)。如图((b))中,(Z)与(X,Y,W)不相连,则我们称这两个集合被空集分离。在图((c))中,(C=X,Z)分离(Y)和(W)。
分离集有良好的性质,它们将图分解成条件独立的部分。
马尔可夫随机场 - 因子分解
最大团
全局马尔可夫性质允许我们将图分解成更小的易控制的片段,因此在计算和解释性上有本质上的简化.基于这个目的,我们将图分解成 团 (clique)。团是一个完全子图——所有顶点都与其他点邻接的顶点集;如果一个团,没有其他顶点可以加进去仍保持是一个团的称为最大团。
在上述((a)、(b)、(c)、(d))四幅图中,对应的最大团为:
- (a) ({X,Y}, {Y,Z})
- (b) ({X,Y,W}, {Z})
- (C) ({X,Y}, {Y,Z}, {Z,W}, {X,W})
- (d) ({X,Y}, {Y,Z}, {Z,W})
概率密度函数
马尔可夫网络中,概率密度函数(f)可以表示成:
其中(C)为最大团的集合,并且正函数(Psi_C)称为团势,就是最大团上的势函数。
引入规范因子(Z)(所有可能取值求和)是为了保证概率(P(Y))构成一个概率分布,势函数因为要求是严格正的,因此通常一般定义为指数函数:
于是概率密度函数的分布形式和指数族分布形式上相同,这个分布其实叫做(Gibbs)分布(玻尔兹曼分布),满足最大熵原理。