CF961G Partitions

https://www.luogu.org/problemnew/show/CF961G

有点自闭，没有想到最后那个地方可以二项式定理qwq

考虑计算每个物品的贡献。

变成求这个式子

套路的拆一下stirling数。。。

然后考虑后面那个东西。。。

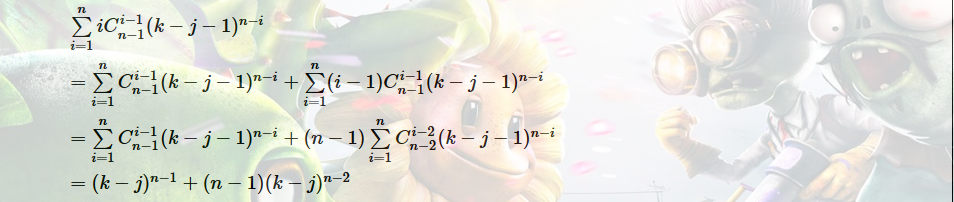
最后这个拆式子的方法有点神仙。。。

#include<bits/stdc++.h>
#define N 1100000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline int read()
{
	char ch=0;
	int x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
const int mo=1e9+7;
int ksm(int x,int k)
{
	int ans=1;
	while(k){if(k&1)ans=1ll*ans*x%mo;k>>=1;x=1ll*x*x%mo;}
	return ans;
}
int inv(int x){return ksm(x,mo-2);}
int fac[N];
int main()
{
	int n=read(),k=read(),t=k-1,tot=0,ans=0;	
	for(int i=1;i<=n;i++)tot=(tot+read())%mo;fac[0]=1;
	for(int i=1;i<=max(n,k);i++)fac[i]=1ll*fac[i-1]*i%mo;
	if(n==1){printf("%d",tot);return 0;}
	for(int i=0;i<=t;i++)
	{
		int x=1ll*ksm(-1,t-i)*inv(fac[t-i])%mo*inv(fac[i])%mo;
		int y=(ksm(i+1,n-1)+(1ll*(n-1)*ksm(i+1,n-2)%mo))%mo;
		ans=(ans+(1ll*x*y%mo))%mo;
	}
	printf("%lld",((1ll*ans*tot%mo)+mo)%mo);
	return 0;
}