图形学基础（一）光栅图形学_上：画直线/圆、区域填充

C++，MFC模板，VS2017

画直线（DDA，中点，Bresenham）

1、DDA画线法

直线方程：y=kx+b

增量处理：y_i+1 = y_i + k

void CLine01View::DDALine()
{
    CDC* pDC = GetDC();
    int x, y, k, _k, dx, dy;
    x = begin.x, y = begin.y;
    dx = end.x - begin.x, dy = end.y - begin.y;
    k = dy / dx, _k = dx / dy;
    if (abs(k) < 1) {//斜率的绝对值小于1
        if (begin.x > end.x) {//从左到右画
            CPoint temp;
            temp = begin;
            begin = end;
            end = temp;
        }
        for (x; x <= end.x; x++) {
            pDC->SetPixel(x, int(y + 0.5), m_color);//四舍五入
            y = y + k;
        }
    }
    else {//大于1
        if (begin.y > end.y) {//从下到上画
            CPoint temp;
            temp = begin;
            begin = end;
            end = temp;
        }
        for (y; y <= end.y; y++) {
            pDC->SetPixel(int(x + 0.5), y, m_color);
            x = x + _k;
        }
    }
    ReleaseDC(pDC);
}

优点：逻辑简单

缺点：k值和四舍五入包含浮点运算

2、中点画线法

 直线方程：F（x,y）= Ax + By + C = 0

避免浮点运算（直接计算中点）：

d0 = A（xi + 1）+ B（yi + 0.5）+ C = 0 + A + 0.5B

增量处理：

d<0时，d1 =  A（xi + 2）+ B（yi + 1.5）+ C = d0 + A + B

d>0时，d2 =  A（xi + 2）+ B（yi + 0.5）+ C = d0 + A 

void CLine01View::MidPointLine()
{
    CDC* pDC = GetDC();
    int A, B, d, d1, d2, x, y;
    if (begin.x > end.x) {//确保begin在左
        CPoint temp;
        temp = begin;
        begin = end;
        end = temp;
    }
    A = begin.y - end.y; B = end.x - begin.x;
    x = begin.x, y = begin.y;
    if (abs(A) < B) {//0<|k|<1
        if (A < 0) {//单调增 k>0
            d = 2 * A + B, d1 = 2 * (A + B), d2 = 2 * A;
            pDC->SetPixel(x, y, m_color);
            while (x < end.x) {
                if (d < 0) { x++, y++, d = d + d1; }
                else { x++, d = d + d2; }
                pDC->SetPixel(x, y, m_color);
            }
        }
        else {//单调减 k<0
            d = 2 * A - B, d1 = 2 * A, d2 = 2 * (A - B);
            pDC->SetPixel(x, y, m_color);
            while (x < end.x) {
                if (d < 0) { x++, d += d1; }
                else { x++, y--, d += d2; }
                pDC->SetPixel(x, y, m_color);
            }
        }
    }
    else {//大斜率 |k|>1
        if (A < 0) {//增 k>0
            d = 2 * B + A, d1 = 2 * B, d2 = 2 * (A + B);
            pDC->SetPixel(x, y, m_color);
            while (y < end.y) {
                if (d > 0) { y++, x++, d += d2; }
                else { y++, d += d1; }
                pDC->SetPixel(x, y, m_color);
            }

        }
        else {//减 k<0
            d = A - 2 * B, d1 = 2 * (A - B), d2 = -2 * B;
            pDC->SetPixel(x, y, m_color);
            while (y > end.y) {
                if (d < 0) { y--, x++, d += d1; }
                else { y--, d += d2; }
                pDC->SetPixel(x, y, m_color);
            }
        }
    }

    ReleaseDC(pDC);
    
}

优点：避免浮点运算

缺点：受直线方程限制

3、Bresenham算法

(有两种解题思路，实操计算，结果都一样，个人感觉 e = k - 0.5 比较好理解)

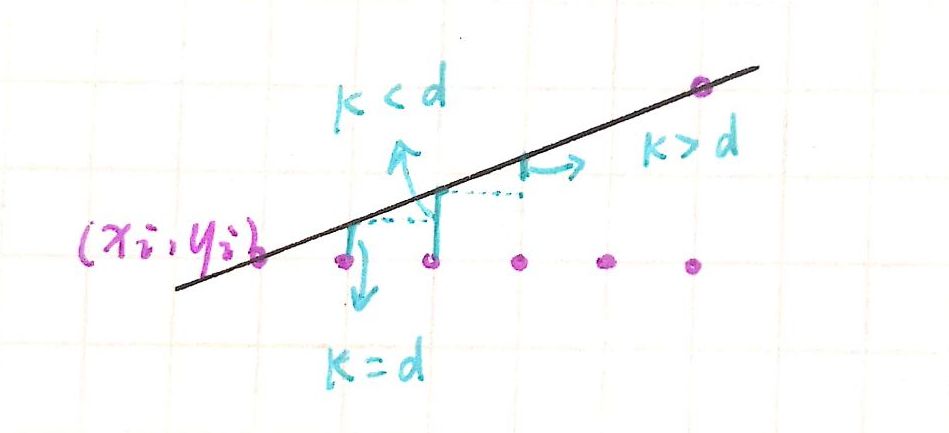
误差项：d = d + k （一旦d >= 1，d = d - 1）

思路：e0 = - 0.5；e = e + k；if（e > 0）e = e - 1；

调整（同时扩大 2dx 倍）：e0 = - dx；e = e + 2dy；if（e > 0）e = e - 2dx；

void CLine01View::BresenhamLine()
{
    CDC* pDC = GetDC();
    int dx, dy, e, x, y;
    dx = abs(end.x - begin.x), dy = abs(end.y - begin.y);
    x = begin.x, y = begin.y;
    int f1, f2, interchange;
    (end.x - begin.x) >= 0 ? f1 = 1 : f1 = -1;
    (end.y - begin.y) >= 0 ? f2 = 1 : f2 = -1;
    if (dy > dx) {//斜率|k|>1 时，=>|_k|
        int temp = dx; dx = dy; dy = temp;
        interchange = 1;
    }
    else {
        interchange = 0;
    }

    e = 2 * dy - dx;
    pDC->SetPixel(x, y, m_color);
    for (int i = 1; i <= dx; i++) {
        if (e >= 0) {
            if (interchange == 1) { x += f1; }    
            else { y += f2; }                
            pDC->SetPixel(x, y, m_color);
            e = e - 2 * dx;
        }
        else {
            if (interchange == 1) { y += f2; }
            else { x += f1; }
            pDC->SetPixel(x, y, m_color);
            e = e + 2 * dy;
        }
    }

    ReleaseDC(pDC);
}

优点：目前来说最好

缺点：不明

画圆（中点，Bresenham）

（条件：第一象限，起点（0，r），圆具有八对称性，椭圆四对称）

 1、中点画圆

圆方程：F（x,y）= x^2 + y^2 - r^2 = 0

计算中点：

d0 = (xi + 1)^2 + (yi + 0.5)^2 + r^2 = 1.25 - r

增量处理：

d<0时，d1 =  (xi + 2)^2 + (yi - 0.5)^2+ r^2 = d0 + 2xi + 3

d>0时，d2 =  (xi + 2)^2 + (yi - 1.5)^2 + r^2 = d0 + 2(xi - yi) + 5

void CLine01View::Midpointcircle()
{
    CDC* pDC = GetDC();
    int xc = begin.x; int yc = begin.y; int r = 50;
    int x, y;
    float d;
    x = 0; y = r; d = 1.25 - r;
while (x <= y) {
        if (d < 0)     d += 2 * x + 3;
        else { d += 2 * (x - y) + 5; y--; }
        x++;
        pDC->SetPixel((xc + x), (yc + y), m_color);
        pDC->SetPixel((xc - x), (yc + y), m_color);
        pDC->SetPixel((xc + x), (yc - y), m_color);
        pDC->SetPixel((xc - x), (yc - y), m_color);
        pDC->SetPixel((xc + y), (yc + x), m_color);
        pDC->SetPixel((xc - y), (yc + x), m_color);
        pDC->SetPixel((xc + y), (yc - x), m_color);
        pDC->SetPixel((xc - y), (yc - x), m_color);
    }
    ReleaseDC(pDC);
}

2、Bresenham画圆

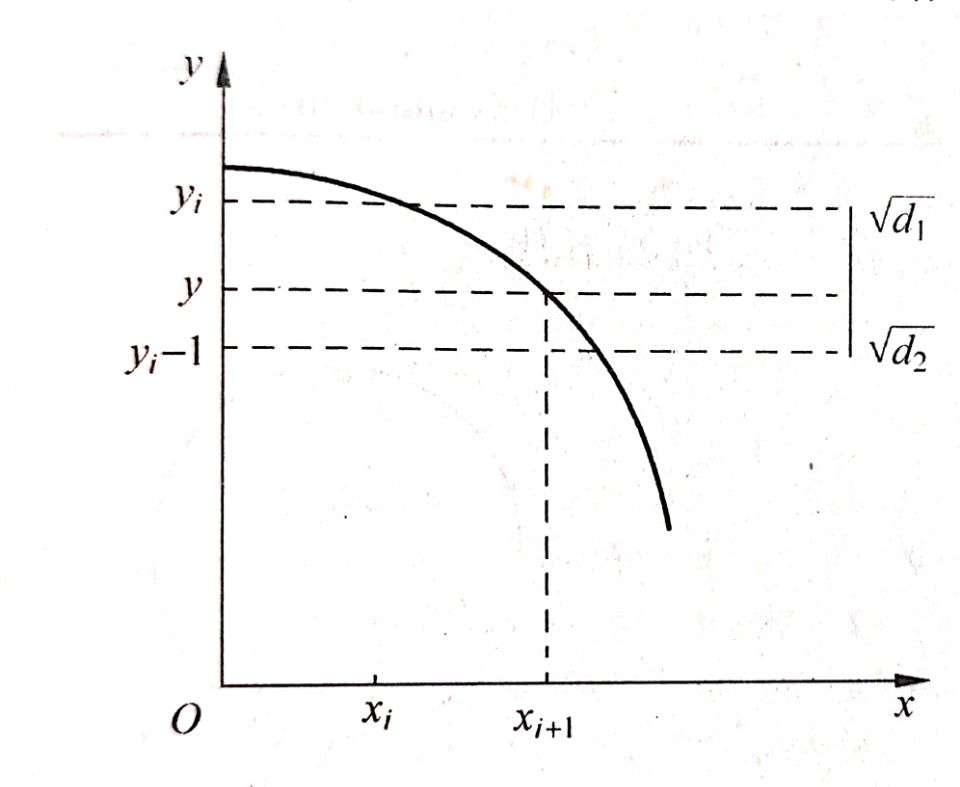
（y^2 = r^2 - (xi + 1)^2 ；d1 = yi^2 - y^2 ；d2 = y^2 - (yi-1)^2 ；）

误差项：pi = d1 - d2 = 2(xi + 1)^2 + yi^2 + (yi - 1)^2 - 2r^2

增量处理：pi+1 = pi + 4xi + 6

void CLine01View::Bresenhamcircle()
{
    CDC* pDC = GetDC();
    int xc = begin.x; int yc = begin.y; int r = 50;
    int x = 0; int y = r; int p = 3 - 2 * r;
    while (x <= y) {
        pDC->SetPixel((xc + x), (yc + y), m_color);
        pDC->SetPixel((xc - x), (yc + y), m_color);
        pDC->SetPixel((xc + x), (yc - y), m_color);
        pDC->SetPixel((xc - x), (yc - y), m_color);
        pDC->SetPixel((xc + y), (yc + x), m_color);
        pDC->SetPixel((xc - y), (yc + x), m_color);
        pDC->SetPixel((xc + y), (yc - x), m_color);
        pDC->SetPixel((xc - y), (yc - x), m_color);
        if (p < 0) { p = p + 4 * x + 6; }
        else { p = p + 4 * (x - y) + 10; y--; }
        x++;
    }
    ReleaseDC(pDC);
}

3、中点算法画椭圆 

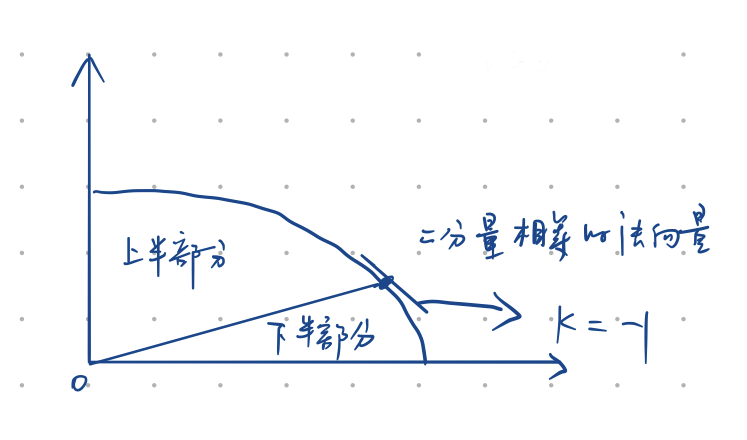
 椭圆公式：F（x,y）= b^2x^2 + a^2y^2 - a^2b^2 = 0

法向量（偏导）：N（x,y）= (dF/dx) i + (dF/dy) j = 2b^2 xi + 2a^2 yi

上半部分：d1 = F（xi + 1，yi - 0.5）

下半部分：d2 = F（xi + 0.5，yi - 1）

void CLine01View::Midpointellispe()
{
    CDC* pDC = GetDC();
    int a = 200, b = 100, xc = begin.x, yc = begin.y;
    int x, y; double d1, d2;
    x = 0, y = b;
    d1 = b * b + a * a*(-b + 0.25);//上半部分
    while (b*b*(x + 1) < a*a*(y - 0.5)) {//法向量
        if (d1 < 0) {    d1 += b * b*(2 * x + 3); }
        else { d1 += b * b*(2 * x + 3) + a * a*(-2 * y + 2); y--; }
        x++;
        pDC->SetPixel((xc + x), (yc + y), m_color);
        pDC->SetPixel((xc - x), (yc + y), m_color);
        pDC->SetPixel((xc + x), (yc - y), m_color);
        pDC->SetPixel((xc - x), (yc - y), m_color);
    }
    d2 = sqrt(b*(x + 0.5)) + a * (y - 1) - a * b;//下半部分
    while (y > 0) {
        if (d2 < 0) { d2 += b * b*(2 * x + 2) + a * a*(-2 * y + 3); x++; }
        else { d2 += a * a*(-2 * y + 3); }
        y--;
        pDC->SetPixel((xc + x), (yc + y), m_color);
        pDC->SetPixel((xc - x), (yc + y), m_color);
        pDC->SetPixel((xc + x), (yc - y), m_color);
        pDC->SetPixel((xc - x), (yc - y), m_color);
    }
    ReleaseDC(pDC);
}

区域填充（扫描、种子）

（条件：凹/凸/内含环 多边形）

void CLine01View::OnLButtonDblClk(UINT nFlags, CPoint point)
{
    // TODO: 在此添加消息处理程序代码和/或调用默认值
    RedrawWindow();
    CDC* pDC = GetDC();
    CPen newpen(PS_SOLID, 1, RGB(255, 0, 0));
    CPen *old = pDC->SelectObject(&newpen);
    spt[0] = CPoint(100, 100);
    spt[1] = CPoint(300, 100);
    spt[2] = CPoint(250, 250);
    spt[3] = CPoint(100, 250);
    spt[4] = CPoint(150, 200);
    spt[5] = CPoint(90, 180);
    spt[6] = CPoint(150, 150);
    spt[7] = CPoint(100, 100);
    pDC->Polyline(spt, 8);
    pDC->SelectObject(old);
    ReleaseDC(pDC);
    for (int i = 0; i < pointCount; i++) {//获取最大和最小点
        maxY = maxY > spt[i].y ? maxY : spt[i].y;
        minY = minY < spt[i].y ? minY : spt[i].y;
    }
}

1、扫描线填充

（比较好理解，但不是最简洁的。“活性边表/新边表”，请参考：https://blog.csdn.net/orbit/article/details/7368996）

此处用 CPtrArray 存放活性边，自定义函数： fill（point_1，point_2）、getCrossPoint（point_0，point_1，y)

void CLine01View::OnScanfill()
{
    // TODO: 在此添加命令处理程序代码
    int crossPointCount = 0;
    CPtrArray ptrPoint;
    for (int y = minY; y < maxY; y += 3) {//对每隔三行的线进行填充
        crossPointCount = 0;//将交点数归零
        ptrPoint.RemoveAll();
        //获取与各边的交点
        for (int i = 1; i < pointCount; i++) {//对每个点进行检查
            if (i < pointCount) {//前count-2个点
                if (y < spt[i - 1].y&&y > spt[i].y || y > spt[i - 1].y&&y < spt[i].y) {
                    crossPointCount++;
                    CPoint p = getCrossPoint(spt[i - 1], spt[i], y);//获得扫描线与多边形的交点
                    //存储点
                    ptrPoint.Add(new CPoint(p.x, p.y));
                }
            }
        }
        if (crossPointCount >= 2) {//填充
            for (int i = 1; i <= crossPointCount; i += 2) {//每两点内为要填充区域
                int x = ((CPoint*)ptrPoint.GetAt(i - 1))->x;
                int y = ((CPoint*)ptrPoint.GetAt(i - 1))->y;
                CPoint p0(x, y);
                x = ((CPoint*)ptrPoint.GetAt(i))->x;
                y = ((CPoint*)ptrPoint.GetAt(i))->y;
                CPoint p1(x, y);
                fill(p0, p1);
            }
        }
    }
}

缺点：数据结构复杂，只适合软件实现

2、注入填充（4-联通，递归）

栈辅助理解：

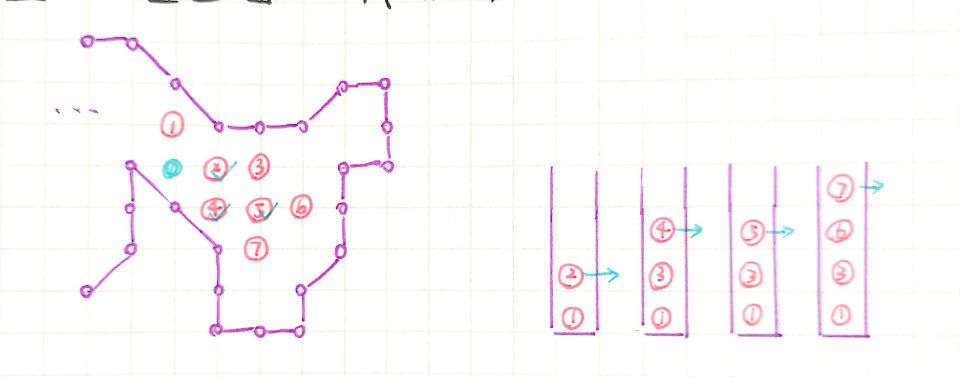
简称：换色 

void CLine01View::floodfill(int x,int y, COLORREF oldcolor, COLORREF newcolor)
{
    CClientDC dc(this);

    if (dc.GetPixel(x,y) == oldcolor) {
        dc.SetPixel(x, y, newcolor);
        floodfill(x, y + 1, oldcolor, newcolor);
        floodfill(x, y - 1, oldcolor, newcolor);
        floodfill(x - 1, y, oldcolor, newcolor);
        floodfill(x + 1, y, oldcolor, newcolor);
    }
}

3、种子扫描线填充（局限）

（hhhh，我自己这么叫的，书上说是种子填充，但是我觉得不严谨）

void CLine01View::OnSeedfill()
{
    // TODO: 在此添加命令处理程序代码
    CDC* pDC = GetDC();
    int color = RGB(0, 255, 0);
    int boundary = RGB(255, 0, 0);
    CPoint pt = s_point;
    
    int x, y;
    x = pt.x; y = pt.y;
    for (; y < maxY; y++) {//下
        int current = pDC->GetPixel(x, y);
        while ((current != boundary) && (current != color)) {//右
            pDC->SetPixel(x, y, color);
            x++;
            current = pDC->GetPixel(x, y);
        }
        x = pt.x;
        x--;
        current = pDC->GetPixel(x, y);
        while ((current != boundary) && (current != color)) {//左
            pDC->SetPixel(x, y, color);
            x--;
            current = pDC->GetPixel(x, y);
        }
        x = pt.x;
    }
    x = pt.x;
    y = pt.y - 1;
    for (; y > minY; y--) {//上
        int current = pDC->GetPixel(x, y);
        while ((current != boundary) && (current != color)) {//左
            pDC->SetPixel(x, y, color);
            x++;
            current = pDC->GetPixel(x, y);
        }
        x = pt.x;
        x--;
        current = pDC->GetPixel(x, y);

        while ((current != boundary) && (current != color)) {//右
            pDC->SetPixel(x, y, color);
            x--;
            current = pDC->GetPixel(x, y);
        }
        x = pt.x;
    }
    
}

4、ex：

扫描种子填充

边填充

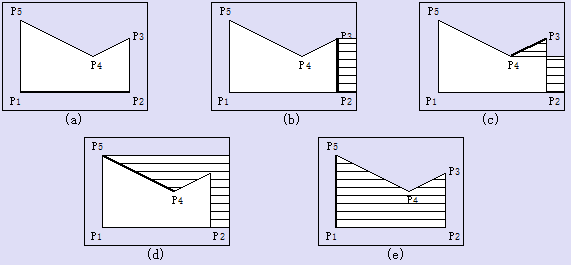
栅栏填充

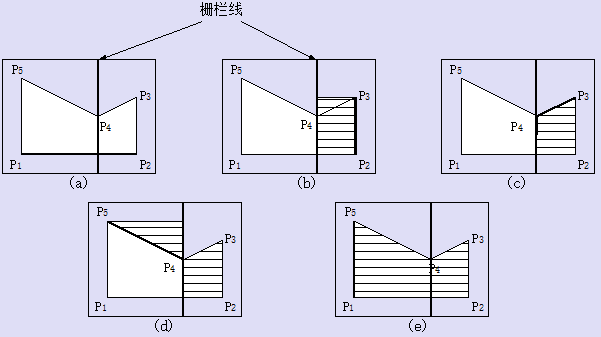
参考资料：

1、《计算机图形学原理及算法教程》和青芳 编著

2、计算机图形学 - 中国农业大学 赵明老师视频 

3、计算机图形学 - 南京工学院 丁宇辰老师讲解

本文采用CC BY 4.0知识共享许可协议。