BZOJ 3529 莫比乌斯反演+树状数组

Description

    有一张N×m的数表，其第i行第j列（1 < =i < =礼，1 < =j < =m）的数值为
能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。

Input

    输入包含多组数据。
    输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。

Output

    对每组数据，输出一行一个整数，表示答案模2^31的值。

Sample Input

2
4 4 3
10 10 5

Sample Output

20
148

HINT

1 < =N．m < =10^5  ， 1 < =Q < =2×10^4

莫比乌斯反演的进阶题. 和平常直接线性筛出答案不同,这个题有a的限制。

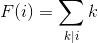，所以：

　　　

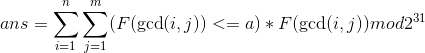
　　　先不考虑a的影响，设：

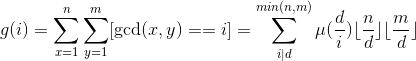          。所以

　　　

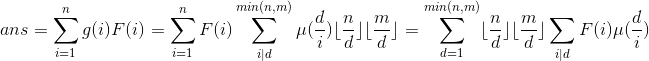
 　　然后考虑询问，

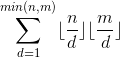　　可以分块，

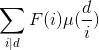　　　，逆向枚举每个合法的i，对其对应的倍数d加上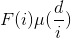，分块的同时查询一下前缀和即可。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <stdio.h>
#define MAXN 100005
#define N 100000
#define full 2147483647
#define ul unsigned int
using std::swap;
using std::min;
bool _prime[MAXN];
int Q,prime[MAXN/10],cnt,mu[MAXN],id[MAXN];
ul sumd[MAXN],s1[MAXN],s2[MAXN],Ans[MAXN];
 
 
template<typename _t>
inline _t read(){
    _t x=0,f=1;
    char ch=getchar();
    for(;ch>'9'||ch<'0';ch=getchar())if(ch=='-')f=-f;
    for(;ch>='0'&&ch<='9';ch=getchar())x=x*10+(ch^48);
    return x*f;
}
 
template<typename _t>
class BIT{
    private:
        _t tree[MAXN];
    public:
        BIT(){memset(tree,0,sizeof tree);}
        inline int lowbit(int x){return x&(-x);}
        inline void Update(int pos,_t val){for(;pos<=N;pos+=lowbit(pos))tree[pos]+=val;}
        inline _t Qsum(int pos){_t ans = 0;for(;pos;pos-=lowbit(pos))ans += tree[pos];return ans;}
};
 
struct Que{
    int x,y,limit,id;
    inline bool operator < (const Que &a)const{return limit < a.limit;}
}q[MAXN];
 
void init(){
    mu[1]=1;id[1]=1;sumd[1]=1;
    for(int i=2;i<=N;i++){
        id[i]=i;
        if(!_prime[i]){
            mu[i]=-1;
            prime[++cnt] = i;
            sumd[i] = i + 1;
            s1[i] = i+1;s2[i]=i;
        }
        for(int j=1;j<=cnt&&prime[j]*i<=N;j++){
            _prime[i*prime[j]]=1;
            if(i%prime[j]==0){
                mu[i*prime[j]] = 0;
                s2[i*prime[j]] = s2[i] * prime[j] ;
                s1[i*prime[j]] = s1[i] + s2[i*prime[j]];
                sumd[i*prime[j]] = sumd[i]/s1[i]*s1[i*prime[j]];
                break;
            }
            mu[i*prime[j]] = -mu[i];
            sumd[i*prime[j]] = sumd[i] * sumd[prime[j]];
            s1[i*prime[j]] = prime[j]+1;
            s2[i*prime[j]] = prime[j];
        }
    }
}
 
BIT<ul>Tree;
inline bool cmp(int x,int y){return sumd[x]==sumd[y]?x<y:sumd[x]<sumd[y];}
inline void change(int now){for(register int i = now;i<=N;i+=now)Tree.Update(i,sumd[now]*mu[i/now]);}
 
inline ul Query(int n,int m){
    if(n>m)swap(n,m);
    int i,last;
    ul ans = 0;
    for(i=1;i<=n;i=last+1){
        last = min(n/(n/i),m/(m/i));
        ans += (Tree.Qsum(last)-Tree.Qsum(i-1))*(m/i)*(n/i);
    }
    return ans & full;
}
 
int main(){
    init();Q=read<int>();
    for(int i=1;i<=Q;i++)q[i].x=read<int>(),q[i].y=read<int>(),q[i].limit=read<int>(),q[i].id=i;
    std::sort(&q[1],&q[Q+1]);std::sort(&id[1],&id[N+1],cmp);
    register int now = 1,i;
    for(i=1;i<=Q;++i){
        while(sumd[id[now]]<=q[i].limit&&now<=N)change(id[now++]);
        Ans[q[i].id] = Query(q[i].x,q[i].y);
    }
    for(int i=1;i<=Q;i++)printf("%d
",Ans[i]);
}