[KD-tree] Luogu P4631 Circle selection

题目描述

在平面上，有 nnn个圆，记为 c1,c2,...,cnc_1, c_2,...,c_nc1​,c2​,...,cn​ 。我们尝试对这些圆运行这个算法：

1. 找到这些圆中半径最大的。如果有多个半径最大的圆，选择编号最小的。记为 cic_ici​。
2. 删除 cic_ici​及与其有交集的所有圆。两个圆有交集当且仅当平面上存在一个点，这个点同时在这两个圆的圆周上或圆内。（原文直译：如果平面上存在一个点被这两个圆所包含，我们称这两个圆有交集。一个点被一个圆包含，当且仅当它位于圆内或圆周上。）
3. 重复上面两个步骤直到所有的圆都被删除。

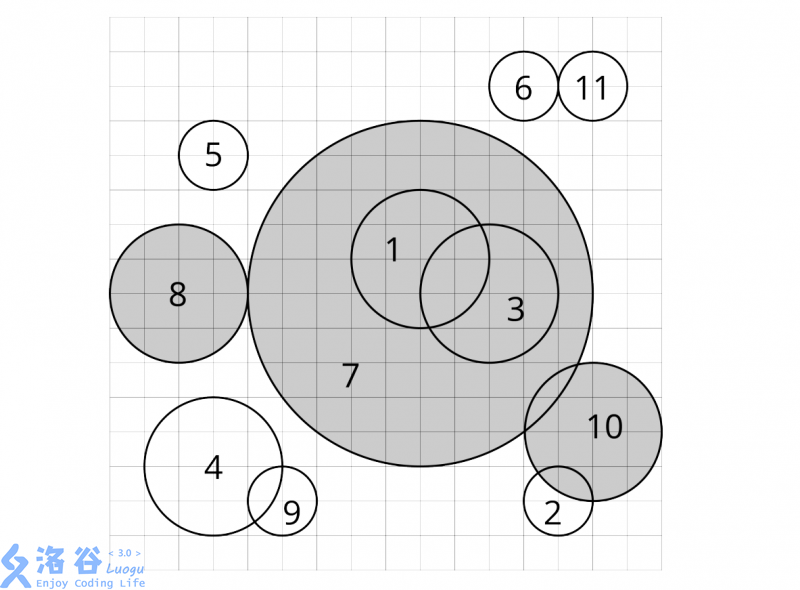
当 cic_ici​被删除时，若循环中第 111步选择的圆是 cjc_jcj​，我们说 cic_ici​被 cjc_jcj​删除。对于每个圆，求出它是被哪一个圆删除的。

题解

• 直接KD-tree乱搞一下啊
• 每个节点维护一下这些圆所在的最小矩形，查的时候如果一个圆被删掉了那就在它的父亲节点里面清除其贡献
• 要转一个角度，不然会被卡

代码

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define N 300010
using namespace std;
const double A=acos(-1)/5,eps=1e-3,inf=1e20;
int n,root,ans[N];
struct node { double x,y,r; int id; }a[N],k;
struct kdtree{node c; double x1,x2,y1,y2; int ls,rs; }t[N];
bool cmp1(node a,node b) { return a.x<b.x; }
bool cmp2(node a,node b) { return a.y<b.y; }
bool cmp(node a,node b) { return a.r==b.r?a.id<b.id:a.r>b.r; }
bool change(int x,int y) { t[x].x1=min(t[x].x1,t[y].x1),t[x].x2=max(t[x].x2,t[y].x2),t[x].y1=min(t[x].y1,t[y].y1),t[x].y2=max(t[x].y2,t[y].y2); }
void pushup(int d)
{
    if (!ans[t[d].c.id]) t[d].x1=t[d].c.x-t[d].c.r,t[d].x2=t[d].c.x+t[d].c.r,t[d].y1=t[d].c.y-t[d].c.r,t[d].y2=t[d].c.y+t[d].c.r; else t[d].x1=t[d].y1=inf,t[d].x2=t[d].y2=-inf;
    if (t[d].ls) change(d,t[d].ls);
    if (t[d].rs) change(d,t[d].rs);
}
int build(int d,int l,int r)
{
    int mid=l+r>>1;
    nth_element(a+l,a+mid,a+r+1,d?cmp1:cmp2),t[mid].c=a[mid];
    if (l<mid) t[mid].ls=build(d^1,l,mid-1);
    if (mid<r) t[mid].rs=build(d^1,mid+1,r);
    pushup(mid); return mid;
}
bool check(node d) { return (d.x-k.x)*(d.x-k.x)+(d.y-k.y)*(d.y-k.y)<=(d.r+k.r)*(d.r+k.r)+eps; }
bool pd(int d) { return t[d].x1>k.x+k.r+eps||t[d].x2+eps<k.x-k.r||t[d].y1>k.y+k.r+eps||t[d].y2+eps<k.y-k.r; }
void query(int d)
{
    if (pd(d)) return;
    if (!ans[t[d].c.id]&&check(t[d].c)) ans[t[d].c.id]=k.id;
    if (t[d].ls) query(t[d].ls);
    if (t[d].rs) query(t[d].rs);
    pushup(d);
}
int main()
{
    scanf("%d",&n);
    for (int i=1,x,y,z;i<=n;i++) scanf("%d%d%d",&x,&y,&z),a[i]=(node){x*cos(A)+y*sin(A),y*cos(A)-x*sin(A),z,i};
    root=build(0,1,n),sort(a+1,a+n+1,cmp);
    for (int i=1;i<=n;i++) if (!ans[a[i].id]) k=a[i],query(root);
    for (int i=1;i<=n;i++) printf("%d ",ans[i]);
}